07 字符串

发表于 2015/02/23 更新于 2025/02/02

作者 Hacket Zeng

45 分钟阅读

07 字符串

字符串基础

必须掌握的字符串题

最长回文子串 medium
最小覆盖子串 hard
无重复字符的最长子串 medium
43.字符串相乘 medium
415.字符串相加 easy

字符串面试题

43. 字符串相乘 medium

题目：

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。输入: num1 = “2”, num2 = “3” 输出: “6”

解法 1：普通竖式乘法 + 字符串相加

思路：

竖式运算思想，以 num1 为 123，num2 为 456 为例分析，num1 是被乘数，num2 是乘数：
遍历 num2 每一位与 num1 进行相乘，将每一步的结果两两进行累加作为下一次的输入
num2 除了第一位的其他位与 num1 运算的结果需要补 0
最后字符串两两相加，那就变成了 415 题的字符串相加问题了

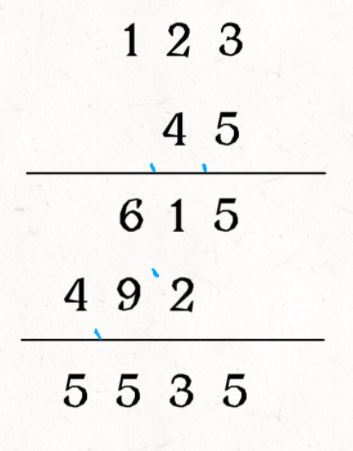
小结：有两个指针 i，j 在 num1 和 num2 上游走，计算乘积，同时将乘积叠加到 res 的正确位置；需要注意乘法进位，加法进位，错位相加几个问题
代码：

  
public String multiply2(String num1, String num2) {
    if (num1.equals("0") || num2.equals("0")) {  // 边界判断
        return "0";
    }
    int n1 = num1.length(); // 123
    int n2 = num2.length(); // 456
    String res = "0"; // 保存结果
    for (int i = n2 - 1; i >= 0; i--) {
        int val2 = num2.charAt(i) - '0';
        StringBuilder sb = new StringBuilder();
        int carry = 0; // 临时记录乘法进位
        for (int j = n1 - 1; j >= 0; j--) {
            int val1 = num1.charAt(j) - '0';
            int count = val1 * val2 + carry;
            sb.insert(0, count % 10);
            carry = count / 10;
        }
        if (carry != 0) {
            sb.insert(0, carry);
        }
        // 错位相加：num2的后几位需要在后面补0
        for (int h = n2 - 1; h > i; h--) {
            sb.append("0");
        }
        res = addStrings(res, sb.toString());
    }
    return res;  // 最后将res相加：变成了求字符串相加了
}
// 字符串相加
public String addStrings(String num1, String num2) {
    if (num1.equals("0")) {
        return num2;
    }
    if (num2.equals("0")) {
        return num1;
    }
    StringBuilder res = new StringBuilder(); // 保存计算结果
    int i = num1.length() - 1;
    int j = num2.length() - 1;
    int carry = 0; // 加法进位
    while (i >= 0 || j >= 0) {
        int temp1 = i >= 0 ? num1.charAt(i) - '0' : 0;
        int temp2 = j >= 0 ? num2.charAt(j) - '0' : 0;
        int temp = temp1 + temp2 + carry;
        res.append(temp % 10); // 个位数的值
        carry = temp / 10; // 进位值
        i--;
        j--;
    }
    if (carry > 0) {
        res.append(carry);
    }
    return res.reverse().toString();
}

复杂度：

时间复杂度：O(M*N)。M,NM,N 分别为 num1 和 num2 的长度
空间复杂度：O(M+N)。用于存储计算结果

解法 2：优化竖式最优解

题解

思路：
竖式计算的结果有一定的规律

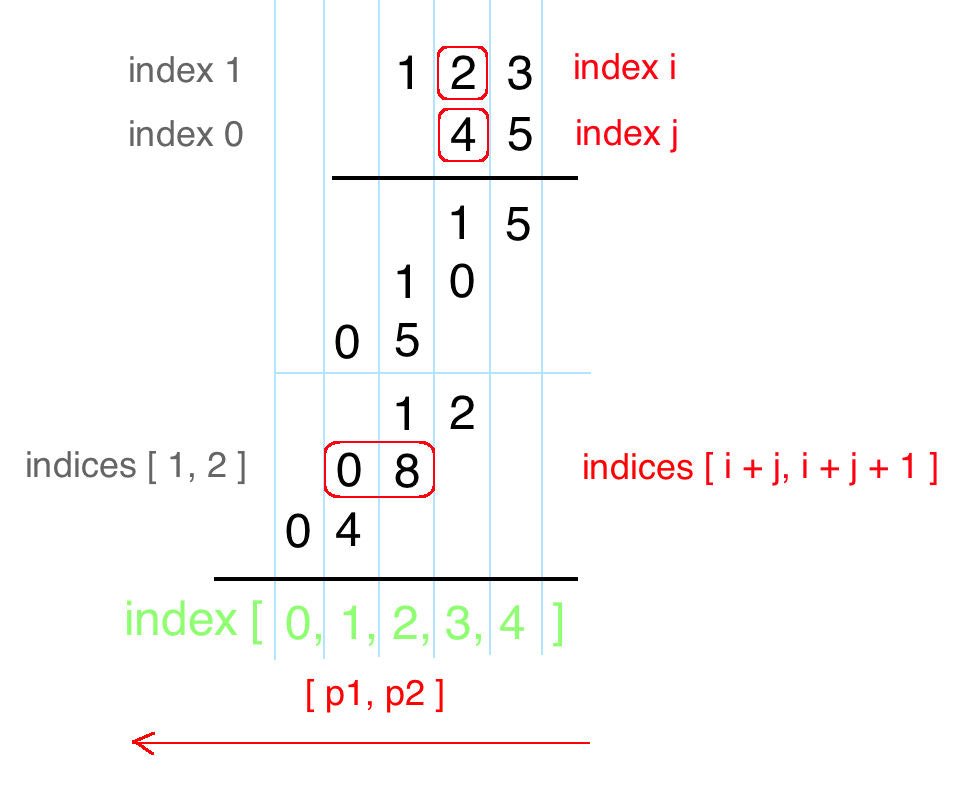
乘数 num1 长度为 M，被乘数 num2 长度为 N，num1 X num2 结果的最大长度为 M+N
num1[i] X num2[j] 的结果第一位位于 res[i+j]，第二位位于 res[i+j+1]
图例

具体实现
- 存储结果的一维 int 数组 res，长度为 num1 和 num2 长度之和
- num1 或 num2 谁作为 i 和 j 都可以
- 倒序遍历 num1 和 num2
  - 首先计算 num1 和 num2 最后一位数相乘
  - 计算 count：将相乘之和和 res[i+j+1] 相加（为什么是 i+j+1？因为 i 和 j 处位置相乘后就存储在该位置，可能该位置已经存储了值，所以要加上 i+j+1 处的值）
  - 计算新的 res[i+j+1] 处的值：count%10
  - 计算新的 res[i+j]，其实就是计算进位值，count/10
- 最后将 res 转成数组，需要把 res 首的 0 过滤掉

代码：

  
public String multiply(String num1, String num2) {
    // 边界判断
    if (num1.equals("0") || num2.equals("0")) {
        return "0";
    }
    // 被乘数j，乘数i，位置第一个元素res[i+j]，第二个元素res[i+j+1]
    int n1 = num1.length(); // 被乘数
    int n2 = num2.length(); // 乘数
    int[] res = new int[n1 + n2];
    for (int i = n2 - 1; i >= 0; i--) {
        int temp1 = num2.charAt(i) - '0';
        for (int j = n1 - 1; j >= 0; j--) {
            int temp2 = num1.charAt(j) - '0';
            // 他们计算的结果第一位在res[i+j]，第二位在res[i+j+1]
            int count = (temp1 * temp2) + res[i + j + 1]; // 相乘+当前计算第二位置原有的值
            // 保存i+j+1处的值，这里不需要累加是因为i+j+1在上面已经参与计算了
            res[i + j + 1] = count % 10;
            // 进位，需要累计前面已经在该位置计算的值
            res[i + j] += count / 10;
        }
    }
    StringBuilder sb = new StringBuilder();
    for (int i = 0; i < res.length; i++) {
        if (i == 0 && res[0] == 0) {
            continue;
        }
        sb.append(res[i]);
    }
    return sb.toString();
}

复杂度：

时间复杂度：O(M*N)。M,NM,N 分别为 num1 和 num2 的长度
空间复杂度：O(M+N)。用于存储计算结果

415.字符串相加 easy

题目：

给定两个字符串形式的非负整数 num1 和 num2 ，计算它们的和并同样以字符串形式返回。你不能使用任何內建的用于处理大整数的库（比如 BigInteger），也不能直接将输入的字符串转换为整数形式。

思路：

解法 1：模拟人工计算双指针

思路：

如果将字符串转换为数字来计算，如果两个比较大的数字相加，可能会溢出；所以我们得换种思路模拟人工计算
计算进位：tmp=n1+n2+carry，carry = tmp/10，表示当前位相加是否产生进位
添加当前位：tmp%10
索引溢出处理：溢出的字符串赋值为 0 去参与运算，相当于给长度较短的前面补 0
头部 carry：跳出循环后，根据 carry 值决定是否在头部添加进位 1
最后反转存储计算结果的字符串

代码 1：

  
public String addStrings(String num1, String num2) {
    int n1 = num1.length();
    int n2 = num2.length();
    // 考虑边界
    if (num1.equals("0")) {
        return num2;
    }
    if (num2.equals("0")) {
        return num1;
    }
    // 记录结果值
    StringBuilder sb = new StringBuilder();
    // 记录索引
    int i = 0;
    // 进位值
    int carry = 0;
    while (i < n1 || i < n2) {
        int temp1 = 0;
        int temp2 = 0;
        if (i < n1) {
            temp1 = num1.charAt(n1 - i - 1) - '0';
        }
        if (i < n2) {
            temp2 = num2.charAt(n2 - i - 1) - '0';
        }
        // 当前i位置的值 = n1和n2在i位置的值+前一位的进位值
        int count = temp1 + temp2 + carry;
        // 只取最后一位
        int val = count % 10;
        // 计算进位
        carry = count / 10;
        sb.append(val);
        i++;
    }
    // 还有进位值，需要加上，如1+9
    if (carry != 0) {
        sb.append(carry);
    }
    return sb.reverse().toString();
}

代码 2：简洁版

  
public String addStrings(String num1, String num2) {
    // 存储结果的
    StringBuilder res = new StringBuilder();
    int i = num1.length() - 1;
    int j = num2.length() - 1;
    int carry = 0;
    while (i >= 0 || j >= 0) { // 倒序遍历
        int n1 = i >= 0 ? num1.charAt(i) - '0' : 0;
        int n2 = j >= 0 ? num2.charAt(j) - '0' : 0;
        int tmp = n1 + n2 + carry;
        res.append(tmp % 10);
        carry = tmp / 10;
        i--;
        j--;
    }
    if(carry > 0) res.append(carry);
    return res.reverse().toString();
}

滑动窗口题

3. 无重复字符的最长子串 medium

2022 荔枝笔试题

题目

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。、输入: s = “abcabcbb” 输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

解法 1：滑动窗口 labuladong

  
public static int lengthOfLongestSubstring(String s) {
    // 记录当前 最长子串 最大长度
    int max = 0;
    // 滑动窗口：保存无重复的字符，key为字符，value为该字符出现的次数，大于1就是重复了
    HashMap<Character, Integer> window = new HashMap<>();
    int left = 0;
    int right = 0;
    while (right < s.length()) {
        char ch = s.charAt(right);
        // 扩大窗口
        right++;
        window.put(ch, window.getOrDefault(ch, 0) + 1);

        // 出现了重复，收缩窗口
        while (window.get(ch) > 1) {
            char ch1 = s.charAt(left);
            window.put(ch1, window.getOrDefault(ch1, 0) - 1);
            left++;
        }
        max = Math.max(max, right - left);
    }
    return max;
}

解法 2：滑动窗口（HashSet）

思路

利用 HashSet 不可以存重复元素的特点，所以我们可以选择 HashSet 来存储遍历到的字符** **
临时遍历 set 保存滑动过程中的字符，如果出现相同的字符，需要调整窗口
使用 HashSet 将字符存储在当前窗口 [i,j) 中。然后我们向右侧滑动索引 j，如果它不在 HashSet 中，我们会继续滑动 ,如果直 s[j] 已经存在于 HashSet 中, 我们需要逐个将 HashSet 中的值 remove , 直到将 j 对应的重复值移出 Set,与此同时,索引 i 右移。
时间复杂度 O(2n)

  
public static int lengthOfLongestSubstring2(String s) {
    int max = 0;
    int left = 0;
    int right = 0;
    HashSet<Character> window = new HashSet<>();
    while (right < s.length()) {
        char c = s.charAt(right);
        if (window.add(c)) { // 无重复字符
            // 计算最长子串最大长度
            max = Math.max(max, right - left + 1);
            // 扩大窗口
            right++;
        } else { // 出现了重复，移除左边
            char ch = s.charAt(left);
            // 收缩窗口
            window.remove(ch);
            left++;
        }
    }
    return max;
}

不足

在窗口滑动的过程中，遇到重复字符了，需要从左逐个从 HashSet 删除直到没有重复字符了；存在字符重复，需要 2n 的遍历

解法 3：滑动窗口 HashMap 优化版（HashMap 保留索引，防止有多个重复元素每次都要移除）推荐

题解：画解算法：3. 无重复字符的最长子串
思路

HashMap 保存字符的索引，避免用 HashSet 出现多个重复字符时需要一个个删除；定义一个 HashMap 数据结构存储 (k, v)map，其中 key 值为字符，value 值为字符位置
我们定义不重复子串的开始位置为 start，结束位置为 end
随着 end 不断遍历向后，往 map 添加字符 ch(key 为字符，value 为字符位置索引 end)；
1. map 中不存在 ch，说明不存在重复字符，直接添加进去，更新 max（取 max 和 end-start+1 最大值）
2. 当 map 中已经存在 ch 了，说明存在了重复字符了，我们只需要从 map 中获取到该 ch 的位置 index，index 及之前添加新的字符的话都是存在重复字符的，从 index+1 位置开始字符不重复，让 start=map[ch]+1
  1. 字符 ch 包含在 map 中，ch 在最新的最长有效无重复子串中，指需要让 start=map[ch]+1
  2. 字符 ch 包含在 map 中，ch 不在最新的最长有效无重复子串中，如 abba，当遍历到第 2 个字符 b 时，end=2，start=1+1=2，此时 ch 不在最长有效子串中，如果 start=map.get(‘a’)+1=0+1=1，实际上此时 start 应该为 2，所以 start 需要取 start 和 map[ch]+1 之间的最大值
3. 无论是否更新 start，都会更新其 map 数据结构和结果 max
4. 返回 max
时间复杂度 O(n)

思考

在窗口滑动的过程中，遇到重复字符了，需要从左逐个从 HashSet 删除直到没有重复字符了；存在字符重复，需要 2n 的遍历；比如字符串是 s=”bbbbbbbb” 这种

代码

HashMap 滑动窗口，出现重复字符时，调整滑动窗口左边界时加 1

  
public static int lengthOfLongestSubstring(String s) {
    //  用map 来存，方便得到每个字符的下标
    HashMap<Character, Integer> map = new HashMap<>();
    int max = 0;
    for (int start = 0, end = 0; end < s.length(); end++) {
        char ch = s.charAt(end);
        if (window.containsKey(ch)) {
            /**
             1、首先，判断当前字符是否包含在map中，如果不包含，将该字符添加到map（字符，字符在数组下标）,
             此时没有出现重复的字符，左指针不需要变化。此时不重复子串的长度为：end-start+1，与原来的max比较，取最大值；

             2、如果当前字符 ch 包含在 map中，此时有2类情况：
             1）当前字符包含在当前有效的子段中，如：abca，当我们遍历到第二个a，当前有效最长子段是 abc，我们又遍历到a，
             那么此时更新 start 为 map.get(a)+1=1，当前有效子段更新为 bca；
             2）当前字符不包含在当前最长有效子段中，如：abba，我们先添加a,b进map，此时start=0，我们再添加b，发现map中包含b，
             而且b包含在最长有效子段中，就是1）的情况，我们更新 start=map.get(b)+1=2，此时子段更新为 b，而且map中仍然包含a，map.get(a)=0；
             随后，我们遍历到a，发现a包含在map中，且map.get(a)=0，如果我们像1）一样处理，就会发现 start=map.get(a)+1=1，实际上，left此时
             应该不变，start始终为2，子段变成 ba才对。

             为了处理以上2类情况，我们每次更新start，start=Math.max(start,map.get(ch)+1).
             另外，更新start后，不管原来的 s.charAt(end) 是否在最长子段中，我们都要将 s.charAt(end) 的位置更新为当前的end，
             因此此时新的 s.charAt(end) 已经进入到 当前最长的子段中。
             */
            start = Math.max(start, map.get(ch) + 1); // 处理abba这种情况，当添加第2个a时，当前字符不在当前最长有序子串中但在window中就会导致计算不对了，所以需要max
        }
        //不管是否更新left，都要更新 s.charAt(i) 的位置！
        map.put(ch, end); // 加入新的字符， 遇到重复的字符会更新在map中的value值，即重复字符的最新下标
        max = Math.max(max, end - start + 1); // 更新最大不重复子串长度
    }
    return max;
}

76. 最小覆盖子串 minimum-window-substring hard

2022 年腾讯 K 歌面试手撕

题目

给出两个字符串 S 和 T，要求在 O(n) 的时间复杂度内在 S 中找出最短的包含 T 中所有字符的子串。
例如：
S =”ADOBECODEBANC”
T =”ABC”
找出的最短子串为 “BANC”. 注：如果 S 中没有包含 T 中所有字符的子串，返回空字符串 ““；满足条件的子串可能有很多，但是题目保证满足条件的最短的子串唯一。

解法 1：变长滑动窗口

思路

采用滑动窗口思路来解题；2 个窗口 window 和 need，都是 HashMap，key 为字符，value 为该字符出现的次数；need 用来存模板字符串 t 所有的字符出现的次数，window 用来遍历字符串 s 过程中，找到了在 t 中的字符出现的次数
left 和 right 双指针，left 指向窗口左边，right 指向窗口右边；
滑动窗口，直到 right 到达字符串 s 末端
1. 扩大窗口：遍历字符串 s 每个字符，窗口不断向右扩大，直到窗口 window 中的字符全部包括了 t 的字符
2. 收缩窗口：移除窗口最左边的字符，找到长度最短的子串
3. 滑动窗口过程中，用变量 valid 变量表示窗口中满足 need 条件的字符个数，如果 valid 和 need.size 的大小相同，则说明窗口已满足条件，已经完全覆盖了串 T。
  1. 当我们发现某个字符在 window 的数量满足了 need 的需要，就要更新 valid，表示有一个字符已经满足要求。而且，你能发现，两次对窗口内数据的更新操作是完全对称的。
  2. 当 valid == need.size() 时，说明 T 中所有字符已经被覆盖，已经得到一个可行的覆盖子串，现在应该开始收缩窗口了，以便得到「最小覆盖子串」。移动 left 收缩窗口时，窗口内的字符都是可行解，所以应该在收缩窗口的阶段进行最小覆盖子串的更新，以便从可行解中找到长度最短的最终结果。

代码

  
public static String minWindow(String s, String t) {
    // 存目标字符的窗口，要考虑重复的字符，不能用HashSet; key存char，value存出现的次数
    HashMap<Character, Integer> need = new HashMap<>();
    // 滑动的窗口; key存char，value存出现的次数
    HashMap<Character, Integer> window = new HashMap<>();

    // 目前字符窗口
    for (int i = 0; i < t.length(); i++) {
        char ch = t.charAt(i);
        need.put(ch, need.getOrDefault(ch, 0) + 1);
    }
    // 窗口左边
    int left = 0;
    // 窗口右边
    int right = 0;
    // 当前已经覆盖了t多少个字符了，当valid达到need.size()需要缩小窗口来求一个解
    int valid = 0;
    // 记录当前最小的区间长度
    int len = Integer.MAX_VALUE;
    // 记录最优子串的起始点
    int start = 0;
    while (right < s.length()) {
        char ch = s.charAt(right);
        // 窗口不停向右扩大
        right++;

        // 不停地往window添加字符
        if (need.containsKey(ch)) {
            // 是t中包含的字符
            window.put(ch, window.getOrDefault(ch, 0) + 1);
            // ch是否是有效的覆盖字符，是的话valid+1
            if (window.get(ch).equals(need.get(ch))) {
                valid++;
            }
        }
        // window已经完全覆盖了need所需字符了，需要缩小窗口得到最优解
        while (valid == need.size()) { // 要写成while不能写成if，否则只会删除一个就退出了
            // 取最小的len
            int temp = right - left;
            if (temp < len) {
                start = left;
                len = temp;
            }
            // d是要被移除的字符
            char d = s.charAt(left);
            // 缩小窗口
            left++;
            // 如果缩小窗口时的字符是在need中，那么需要更新窗口；否则不需要处理移动left即可
            if (need.containsKey(d)) {
                if (window.get(d).equals(need.get(d))) {
                    valid--;
                }
                window.put(d, window.getOrDefault(d, 0) - 1);
            }
         }
    }
    return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);
}

567. 字符串的排列 medium

题目

给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。换句话说，s1 的排列之一是 s2 的子串。输入：s1 = “ab” s2 = “eidbaooo” 输出：true 解释：s2 包含 s1 的排列之一 (“ba”).

解法 1：定长的滑动窗口

思路

采用滑动窗口思路来解
s1 的字符串是有重复的，题目难度不小
和最小覆盖子串区别是：收缩窗口的时机不一样，s2 包含 s1 的字符串是连续的，当 right-left 超过 s1 长度时，就需要收缩窗口的，直到 s2 字符串遍历完毕或找到了符合排列的子串
这道题中 [left, right) 其实维护的是一个定长的窗口，窗口大小为 t.size()。因为定长窗口每次向前滑动时只会移出一个字符，所以可以把内层的 while 改成 if，效果是一样的。

代码

  
public static boolean checkInclusion(String s1, String s2) {
    // 目标需要的字符
    HashMap<Character, Integer> need = new HashMap<>();
    for (int i = 0; i < s1.length(); i++) {
        char c = s1.charAt(i);
        need.put(c, need.getOrDefault(c, 0) + 1);
    }
    // 滑动窗口
    HashMap<Character, Integer> window = new HashMap<>();
    int left = 0;
    int right = 0;
    int valid = 0;
    while (right < s2.length()) {
        char ch = s2.charAt(right);
        right++;
        if (need.containsKey(ch)) {
            // 扩大窗口：只有存在于need
            window.put(ch, window.getOrDefault(ch, 0) + 1);
            if (window.get(ch).equals(need.get(ch))) {
                // 匹配到了一个字符
                valid++;
            }
        }
        // 什么时候收缩窗口？
        // 因为s2包含s1的字符是连续的，所以当right-left超过了s1的长度时，就要收缩窗口
        while (right - left >= s1.length()) { // 用if也可以，每次只移除一个元素
            // s2包含了s1所有的字符，返回true
            if (valid == need.size()) {
                return true;
            }
            // 收缩窗口
            char c = s2.charAt(left);
            left++;
            if (need.containsKey(c)) {
                if (need.get(c).equals(window.get(c))) {
                    valid--;
                }
                window.put(c, window.getOrDefault(c, 0) - 1);
            }
        }
    }
    return false;
}

字符串反转

344. 反转字符串(反转所有字符串) easy

给定字符串 “abc123”，将该字符串进行反转，得到 “321cba”？不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

解法 1：双指针最优解

  
public void reverseString(char[] s) {
    int m = 0;
    int n = s.length - 1;
    while (m < n) {
        char temp = s[m];
        s[m] = s[n];
        s[n] = temp;
        m++;
        n--;
    }
}

反转不可变列表 (List)

  
public List<Integer> reverseList(List<Integer> list) {
    final int size = list.size();
    List<Integer> reversedList = new ArrayList<>();
    for (int i = 0; i < size; i++) {
        // 把元素i添加到位置0
        reversedList.add(0, list.get(i));
    }
    return reversedList;
}

  
// 原地反转：删除最后一个，插入到i位置，i位置不停的增加，其实就是把最后一个依次从0添加，直到都添加完毕，就反转了
public List<String> listReverse(List<String> list) {
    for (int i = 0, j = list.size() - 1; i < j; i++) {
        System.out.println("i=" + i + ",j=" + j + ",list=" + list);
        list.add(i, list.remove(j));
    }
    return list;
}

541. 反转字符串 II(每2k个字符反转前k个) easy

题目

字符串 s，每隔 2k 个字符反转前 k 个字符，剩余字符少于 k 个，将剩余字符全部反转，如果剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符，其余字符保持原样

解法 1：双指针

思路

使用双指针 l 和 r，l 和 r 两个指针分别圈出每次需要反转的范围
每次反转更新 l 和 r
需要注意 r 不要超过 n-1

题解
这次反转的字符串，不简单。
代码

  
// 解法2：双指针，交换元素temp元素
public static String reverseStr(String s, int k) {
    char[] chars = s.toCharArray();
    int n = s.length();
    // 每2k一组char进行反转
    for (int i = 0; i < n; i += 2 * k) {
        int l = i;
        // 防止r大于了n-1：剩余字符数少于k个了，则全部反转了
        int r = Math.min(l + k - 1, n - 1);
        while (l < r) {
            char temp = chars[l];
            chars[l] = chars[r];
            chars[r] = temp;
            l++;
            r--;
        }
    }
    return String.valueOf(chars);
}

// 解法1：双指针，交换元素异或，效率高
public String reverseStr2(String s, int k) {
    char[] ch = s.toCharArray();
    for(int i = 0; i < ch.length; i += 2 * k){
        int start = i;
        //这里是判断尾数够不够k个来取决end指针的位置
        int end = Math.min(ch.length - 1, start + k - 1);
        //用异或运算反转 
        while(start < end){
            ch[start] ^= ch[end];
            ch[end] ^= ch[start];
            ch[start] ^= ch[end];
            start++;
            end--;
        }
    }
    return new String(ch);
}

151. 反转字符串中的单词 medium

题目

给你一个字符串 s ，请你反转字符串中单词的顺序。单词是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的单词分隔开。返回单词顺序颠倒且单词之间用单个空格连接的结果字符串。 注意：输入字符串 s 中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格

解法 1：双指针

思路

移除首尾和中间多余空格
将整个字符串反转
将每个单词反转，需要注意遍历到最后一个字符的处理

代码

  
public static String reverseWords(String s) {
    // 1、移除首尾、中间空格
    StringBuilder sb = removeSpace(s);
    // 2、反转整个字符串
    reverse(sb, 0, sb.length() - 1);
    // 3、反转每个单词
    reverseEachWord(sb);
    return sb.toString();
}
// 碰到空格就反转每个单词
private static void reverseEachWord(StringBuilder sb) {
    int start = 0;
    int end = start + 1;
    int n = sb.length(); // 不能是sb.length()-1，因为要遍历到最后一个，否则最后一个字母反转不过来
    while (end <= n) { 
        // 遇到空格或者到达最后位置sb.length
        // sb.charAt(end)!=' '用来处理遇到空字符串时就反转
        // end<n 用来处理遍历字符串到最后
        if (end < n && sb.charAt(end) != ' ') { 
            end++;
            continue;
        }
        reverse(sb, start, end - 1);
        start = end + 1;
        end = end + 1;
    }
}
// 反转区间字符串
private static void reverse(StringBuilder sb, int start, int end) {
    while (start < end) {
        char temp = sb.charAt(start);
        sb.setCharAt(start, sb.charAt(end));
        sb.setCharAt(end, temp);
        start++;
        end--;
    }
}
// 移除s中首尾及中间多余的空格
private static StringBuilder removeSpace(String s) {
    StringBuilder sb = new StringBuilder();
    int start = 0;
    int end = s.length() - 1;
    while (s.charAt(start) == ' ') {
        start++;
    }
    while (s.charAt(end) == ' ') {
        end--;
    }
    while (start <= end) {
        char ch = s.charAt(start);
        if (ch != ' ' || sb.charAt(sb.length() - 1) != ' ') {
            sb.append(ch);
        }
        start++;
    }
    return sb;
}

回文数相关

扩展： lc9 回文数、lc5 最长回文子串、lc516 最长回文子序列、lc647 回文子串

9. 回文数 easy

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。

解法 1：转为字符串

  
public static boolean isPalindrome2(int x) {
    String temp = x + "";
    char[] chars = temp.toCharArray();
    int start = 0;
    int end = chars.length - 1;
    while (start < end) {
        if (chars[start] != chars[end]) {
            return false;
        }
        start++;
        end--;
    }
    return true;
}

解法 2：反转数字

  
public static boolean isPalindrome(int x) {
    // 负数，肯定不是回文数
    if (x < 0)
        return false;
    int cur = 0;
    int num = x;
    while (num != 0) { // 不停地的除以10，当为0表示x遍历完毕了
        cur = cur * 10 + num % 10; // num%10，表示得到num个位数; cur*10，需要加上上一位的值
        num = num / 10;
    }
    return cur == x;
}

5. 最长回文子串 medium

题目

给你一个字符串 s，找到 s 中最长的回文子串。 输入：s = “babad” 输出：“bab” 解释：“aba” 同样是符合题意的答案。

解法 1：暴力解法 O(n^3)

思路
列举所有的子串，判断是否为回文串 (首尾双指针法)，保存最长的回文串
代码

  
public static String longestPalindrome(String s) {
    int n = s.length();
    String ams = "";
    int max = 0;
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            // 计算每个子串是否回文结构，并保存最大值
            String temp = s.substring(i, j);
            if (!isPalindromic(temp)) {
                continue;
            }
            if (temp.length() > max) {
                ams = temp;
            }
            max = Math.max(max, temp.length());
        }
    }
    return ams;
}
public static boolean isPalindromic(String s) {
    // 双指针
    int start = 0;
    int end = s.length() - 1;
    while (start < end) {
        if (s.charAt(start) != s.charAt(end)) {
            return false;
        }
        start++;
        end--;
    }
    return true;
}

复杂度

时间复杂度：两层 for 循环 O(n²)，for 循环里边判断是否为回文 O(n)，所以时间复杂度为 O(n³)。
空间复杂度：O(1)

解法 2：动态规划

解法 3：中心扩散法

动态规划、中心扩散、Manacher 算法
思路
中心扩散法的基本思想是：遍历每一个下标，以这个下标为中心，利用回文串中心对称的特点，往两边扩散，看最多能扩散多远；
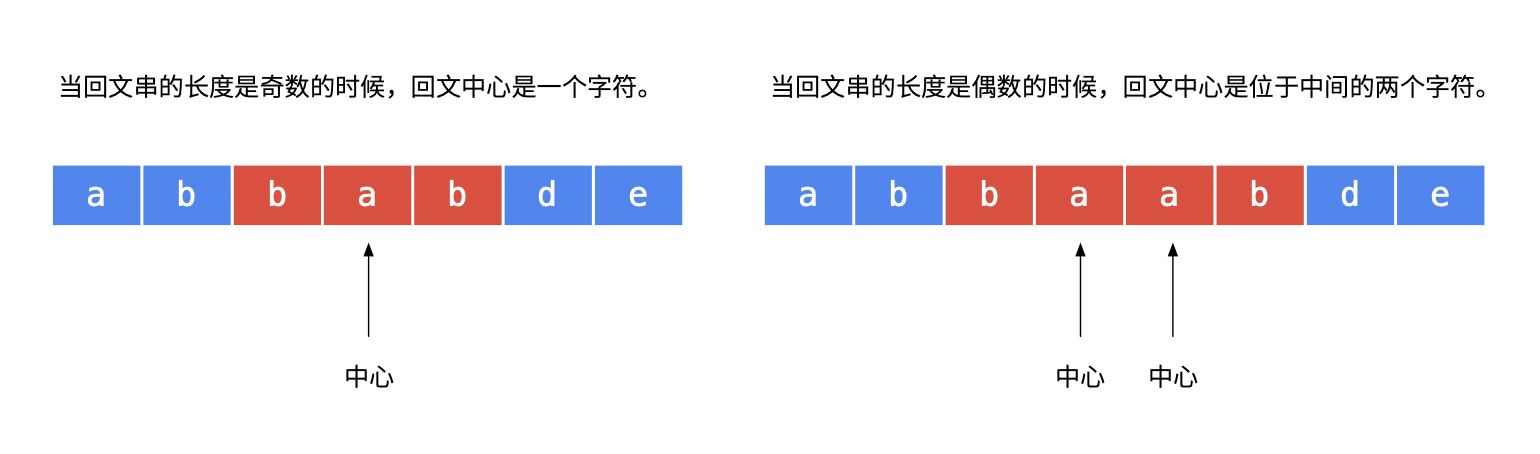
要分回文串长度是奇数还是偶数，回文中心的形态不一样。

奇数回文串的中心是一个具体的字符，例如：回文串 “aba” 的中心字符串是 b
偶数回文串的中心是位于中间的两个字符的空隙，例如：回文串 “abba” 的中心是两个 b，也可以看成是两个 b 中间的空隙

我们可以设计一个方法，兼容以上两种情况：

如果传入重合的下标，进行中心扩散，此时得到的回文子串的长度是奇数；
如果传入相邻的下标，进行中心扩散，此时得到的回文子串的长度是偶数。

代码

  
public static String longestPalindrome2(String s) {
    int n = s.length();
    if (n < 2) return s;
    // 记录目前最大长度的回文子串
    int maxLen = 0;
    // 记录目前最大回文串数组：数组第一位记录起始位置，第二位记录长度
    int[] r = new int[2];
    for (int i = 0; i < n; i++) {
        // 奇数回文扩散
        int[] odd = centerSpread(s, i, i);
        // 偶数回文扩散
        int[] even = centerSpread(s, i, i + 1);
        int[] max = odd[1] > even[1] ? odd : even; // 取它们之间最大的
        // 如果当前回文串长度大于maxLen
        if (max[1] > maxLen) {
            maxLen = max[1]; // maxLen重新赋值
            r = max; // 记录下当前最长回文串的数组
        }
    }
    return s.substring(r[0], r[0] + r[1]); // 截图子串
}

/**
 * 判断一个字符串是否回文
 * @param s     待判断的字符串
 * @param left  扩散的点left
 * @param right 扩散的点right
 * @return 返回一个数组，arr[0]为回文字符串的起始位置，arr[1]为回文字符串的长度
 */
private static int[] centerSpread(String s, int left, int right) {
    int n = s.length();
    while (left >= 0 && right < n) {
        if (s.charAt(left) != s.charAt(right)) {
            break;
        }
        left--; // 向左扩散
        right++; // 向右扩散
    }
    // 因为left和right不满足条件时，已经+或-去了，所以计算起始位置时，left+1，计算长度时right-1-left即可
    return new int[]{left + 1, right - left - 1};
}

复杂度

时间复杂度 O(n^2)
空间复杂度 O(1)

647.回文子串

题目

给你一个字符串 s ，请你统计并返回这个字符串中回文子串的数目。回文字符串是正着读和倒过来读一样的字符串。子字符串是字符串中的由连续字符组成的一个序列。具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。 输入：s = “aaa” 输出：6 解释：6 个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

1、中心法扩散

中心拓展
思路

中心扩散说白了就是挨个遍历
我们可以以 1 个中心点扩散；也可以以 2 个中心点扩散
中心可能是 1 个字符也可能是 2 个字符而已，不可能出现 3 个字符作为中心的情况，因为 3 个字符作为中心的话，他就是回文了，等于 1 个字符作为中心的情况；也不可能以 4 个为中心，4 个等同于 2 个字符的

代码

  
public static int countSubstrings(String s) {
    int len = s.length();
    int ams = 0;
    for (int i = 0; i < len; i++) {
        // 1个点扩散：以letters[i]为中心向两边扩
        //            int m = i - 1;
        //            int n = i + 1;
        int m = i;
        int n = i;
        while (m >= 0 && n < len && s.charAt(m) == s.charAt(n)) {
            ams++;
            m--;
            n++;
        }

        // 2个点扩散：// 以letters[i]右侧的空白位置为中心向两边扩
        int a = i;
        int b = i + 1;
        while (a >= 0 && b < len && s.charAt(a) == s.charAt(b)) {
            a--;
            b++;
            ams++;
        }
    }
    return ams;
}

复杂度
时间复杂度是 O(N^2)，空间复杂度是 O(1)。

字符串匹配 KMP

数据结构和算法, 基础

字符串数据结构和算法

本文由作者按照 CC BY 4.0 进行授权

字符串基础

必须掌握的字符串题

字符串面试题

43. 字符串相乘 medium

解法 1：普通竖式乘法 + 字符串相加

解法 2：优化竖式 最优解

415.字符串相加 easy

解法 1：模拟人工计算 双指针

滑动窗口题

3. 无重复字符的最长子串 medium

解法 1：滑动窗口 labuladong

解法 2：滑动窗口（HashSet）

解法 3：滑动窗口 HashMap 优化版（HashMap 保留索引，防止有多个重复元素每次都要移除）推荐

76. 最小覆盖子串 minimum-window-substring hard

解法 1：变长滑动窗口

567. 字符串的排列 medium

解法 1：定长的滑动窗口

字符串反转

344. 反转字符串(反转所有字符串) easy

解法 1：双指针 最优解

反转不可变列表 (List)

541. 反转字符串 II(每2k个字符反转前k个) easy

解法 1：双指针

151. 反转字符串中的单词 medium

解法 1：双指针

回文数相关

9. 回文数 easy

解法 1：转为字符串

解法 2：反转数字

5. 最长回文子串 medium

解法 1：暴力解法 O(n^3)

解法 2：动态规划

解法 3：中心扩散法

647.回文子串

1、中心法扩散

字符串匹配 KMP

热门标签

解法 2：优化竖式最优解

解法 1：模拟人工计算双指针

解法 1：双指针最优解