03 排序

冒泡排序

冒泡排序思路

1. 有 n 个数，需要 i=n-1 趟排序，每趟需要比较 i 次
2. 每趟前面的数和后面的数做比较，前面的数如果比后面的大，那么两两进行交换，大的数冒泡到后面去
3. 每趟将最大的值冒泡到最后一个位置去

举例子

以 3412 为例，需要 n-1=3 趟冒泡 第 1 趟 (0n-1 03)：3124，将 4 冒泡到这趟的最后 第 2 趟 (0n-2 02)，1234，将 3 冒泡到这趟的最后 第 3 趟 (0~n-1 0-1)，1234，将 2 冒泡到这趟的最后

代码

public static void bubbleSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    // 以3412为例
    // 0~N-1 0~3
    // 0~N-2 0~2
    // 0~N-3 0~1
    int N = arr.length;
    // 由于每趟排序后最后一个元素为最大值，即下趟排序后不参与了，所以控制趟数的end用倒序来控制
    for (int end = N - 1; end >= 0; end--) {
        for (int j = 0; j < end; j++) { // 每趟两个数两两进行比较，前面大的数交换到后面去
            if (arr[j] > arr[j + 1]) {
                swap(arr, j, j + 1);
            }
        }
    }
}

选择排序

选择排序思路

1. 有 n 个数，选择排序需要 i=n-1 趟选择
2. 选择排序每次选择一个最小的值，放在最前面
3. 选择的过程中，默认第 0 个位置的元素为最小值，只更新最小值的索引，在每趟结束后，将最小的值和每趟的第 0 个元素交换位置

代码

public static void selectionSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    int N = arr.length;
    for (int i = 0; i < N - 1; i++) { // 控制趟数
        int minValueIndex = i; // 记录最小值的索引
        for (int j = i + 1; j < N; j++) { // 每趟，默认第0个元素为最小值
            if (arr[j] < arr[minValueIndex]) {
                minValueIndex = j;
            }
        }
        swap(arr, i, minValueIndex);
    }
}

插入排序

排入排序思路

类比抓扑克牌，先来一张牌，将该牌插入到前面已经排好序的牌中去

1. n 个数，需要 n-1 趟插入排序
2. 默认每趟的第 0 个元素已经排好序了
3. 每次往后取下一个元素和前面已经排好序的进行比较，如果比前面的小，交换位置；继续往前走，直到遇到比其大的值或者到边界了

代码实现

public static void insertionSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    int N = arr.length;
    for (int i = 0; i < N - 1; i++) { // 控制躺数
        for (int j = i + 1; j > 0; j--) { // 从排好序的下一个，倒序的
            if (arr[j] < arr[j - 1]) { // 如果后面的元素比前面的小，交换位置，继续往前走
                swap(arr, j, j - 1);
            } else { // 只要后面的比前面的小，终止循环，因为前面的已经是有序的，没必要再做笔记，因为都会比他小
                break;
            }
        }
    }
}

归并排序 （大厂常考）

堆排序 （大厂常考）

思路 (升序为例)：将数组构建为一个大顶堆，首元素即为数组最大值，首尾元素交换；排除末尾元素后调整大顶堆，则新的首元素即为次最大值，交换首尾并再排除末尾元素；如此循环，最后的数组即为升序排列。

public class HeapSort02 {
    public static void main(String []args){
        int []arr = {2,1,8,6,4,7,3,0,9,5};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void sort(int []arr){
        int len = arr.length;
        // 创建一个大顶堆
        for(int i = (int) Math.ceil(len/2 - 1); i >= 0; i--){
            //从第一个非叶子结点从下至上，从右至左调整结构
            adjustHeap(arr,i,len);
        }
        // 交换首尾元素，并重新调整大顶堆
        for(int j = len-1;j > 0;j--){
            swap(arr,0,j);
            adjustHeap(arr,0,j);
        }
    }

    /** 迭代写法*/
    public static void adjustHeap(int []arr,int i,int length){
        int temp = arr[i];
        for (int k = 2*i + 1; k < length; k=k*2 + 1) {
        // 注意这里的k + 1 < length
            // 如果右子节点大于左子节点，则比较对象为右子节点
            if (k + 1 < length && arr[k] < arr[k+1]){
                k++;
            }
            if (arr[k] > temp){
                // 不进行值交换
                arr[i] = arr[k];
                i = k;
            }
            else{
                break;
            }
        }
        arr[i] = temp;
    }

    /** 递归写法*/
    private static void adjustHeap2(int[] arr, int i, int len){
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int maxIndex = i;
        // 注意这里的 left < len
        if (left < len && arr[left] > arr[maxIndex]){
            maxIndex = left;
        }
        if (right < len && arr[right] > arr[maxIndex]){
            maxIndex = right;
        }
        if (maxIndex != i){
            swap(arr,i,maxIndex);
            adjustHeap2(arr,maxIndex,len);
        }
    }

    /** 交换元素 */
    public static void swap(int []arr,int a ,int b){
        int temp=arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
}

快速排序 （大厂常考）

全名 K 歌二面

• 快速排序详解及应用

快速排序小结

一句话总结快速排序：快速排序是先将一个元素排好序，然后再将剩下的元素排好序。

什么是快速排序？

快速排序是对冒泡排序的一种改进。快速排序由 C.A.R. Hoare 在 1960 年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

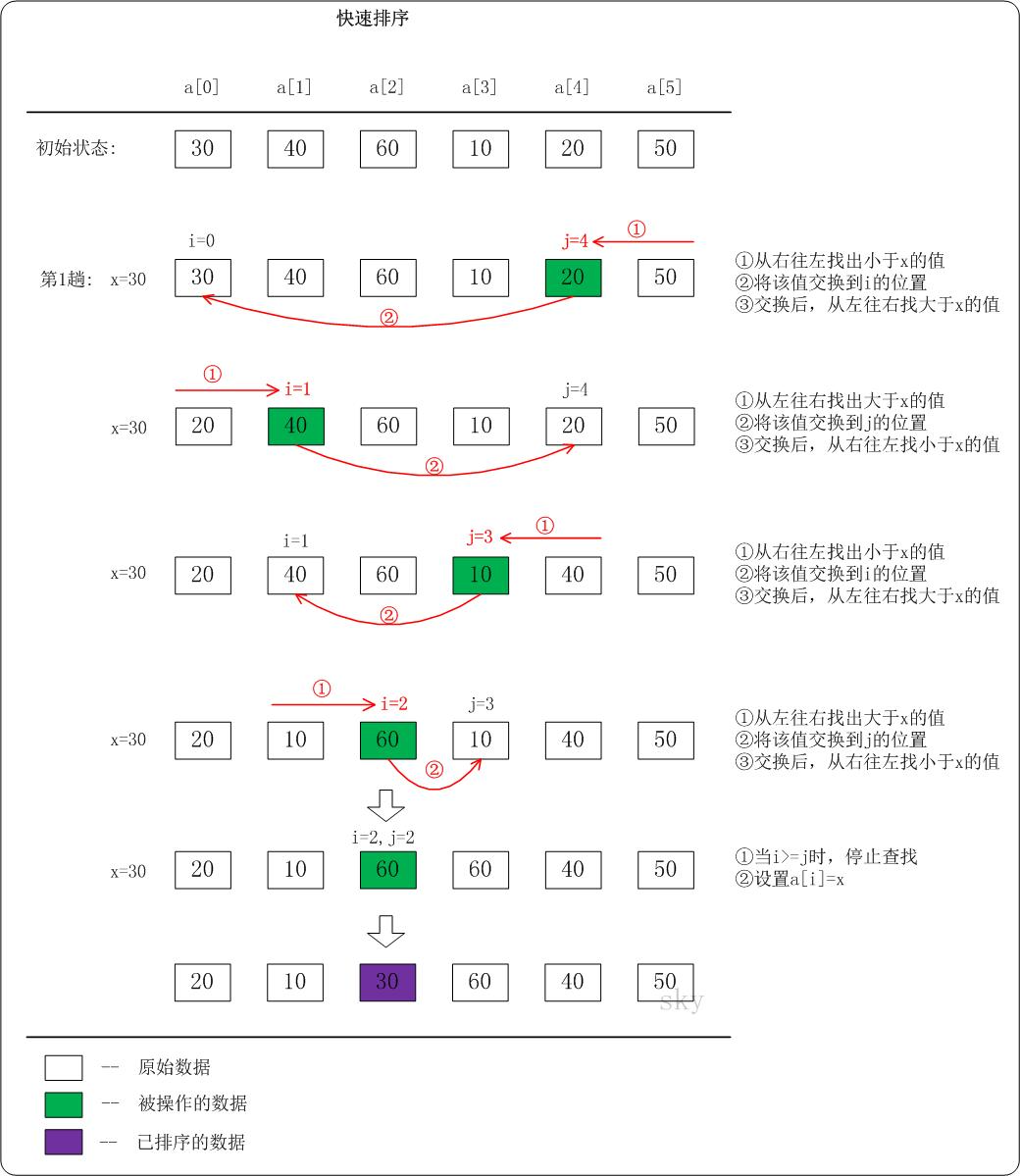
快速排序原理

快速排序几种实现

1. 基本：把等于切分元素的所有元素分到了数组的同一侧，可能会造成递归树倾斜；
2. 双指针：把等于切分元素的所有元素等概率地分到了数组的两侧，避免了递归树倾斜，递归树相对平衡；
3. 三指针（三路块排）：把等于切分元素的所有元素挤到了数组的中间，在有很多元素和切分元素相等的情况下，递归区间大大减少。

pivot 如何选择？

1. pivot 选择最左边，先右指针；pivot 选择最右边，先左指针
2. pivot 随机？

基本的快速排序

基本的快排实现，pivot 选择 low

基本快速排序可分为以下几步

1. 在数组中选择一个基准值（通常为数组的第一个）
2. 将数组中小于基准数的数据移动到基准数左边，大于基准数的移到右边（一次快排 partition）
3. 对于基准数左右两边的数组，不断重复以上两个过程，直到每个子集只有一个元素，即为全部有序

** 如何将一个数组以基准数为中心分为两部分呢？**

在数组的头部和尾部分别设置一个哨兵，它们同时向对方走去，尾部的哨兵如发现有比基准数小的数就停下，头部的哨兵如发现有比基准数大的数就停下，然后交换两个数；再重新走重复前面的交换流程，直到 2 个哨兵相遇，最后交换基准数和尾哨兵。

案例：
有一数组为 6 1 2 7 9 3 4 5 10 8，带着这样做为什么可以的态度来看一下演示。

1. 6 为基准数，设 i，j 为两哨兵，目前指向首尾两个数（加粗部分）

6 1 2 7 9 3 4 5 10 8

1. 两哨兵分别走向对方，直到遇到交换条件，并做交换。

6 1 2 7 9 3 4 5 10 8
6 1 2 5 9 3 4 7 10 8

1. 此时来观察交换后的队列，除去基准数，是不是哨兵走过的位置都已部分有序了呢？ 左边 1 2 5 都比基准数小，右边 7 10 8 都比基准数大。

1 2 5 9 3 4 7 10 8、

1. 继续走直到头尾哨兵相遇，基准数和尾节点交换

6 1 2 5 9 3 4 7 10 8
6 1 2 5 4 3 9 7 10 8
6 1 2 5 4 3 9 7 10 8
3 1 2 5 4 6 9 7 10 8

注意

1. 若以第一个元素为基准数，在哨兵互走过程需右边的哨兵先走。

哨兵互走交换的过程就是不断排序的过程。若右边的哨兵先走，不管走多少次，最后相遇时的那个数是小于基准数的。这时与基准数交换，正好分为两个序列。可若是左边的先走，相遇在大于基准数上就不好办了。

图解
第 1 趟快速排序的流程

代码

public static void quickSort(int[] arr) {
    // 边界判空
    if (arr == null || arr.length <= 1) {
        return;
    }
    quickSort(arr, 0, arr.length - 1);
}
private static void quickSort(int[] arr, int left, int right) {
    // 递归结束条件，如果不是>=而是>也是可以的，只是会多处一些无用的判断而已
    if (left >= right) {
        return;
    }
    // partition，将一个范围内的数组进行原地排序
    int partitionIndex = partition(arr, left, right);
    System.out.println("quickSort partitionIndex=" + partitionIndex + "，left=" + left + "，right=" + right);
    // 递归：将pivot左半边和右半部分都排序
    quickSort(arr, left, partitionIndex - 1);
    quickSort(arr, partitionIndex + 1, right);
}
private static int partition(int[] arr, int low, int high) {
    // 默认选择low作为pivotIndex
    int pivotIndex = low;
    int pivot = arr[pivotIndex];

    // 将比pivot的小的放左边，比pivot大的放右边
    while (low < high) {
        // 一定要从high开始，否则会排序不对
        // 从high开始，往左找一个比pivot的小的值
        // 一定要小于等于，[0, 3, 3, 2, 6, 5, 8, 10, 2]，就会出现low=0,high=1，程序走不下去了
        while (low < high && arr[high] >= pivot) {
            high--;
        }
        // 从low开始，往右找一个比pivot的大的值
        while (low < high && arr[low] <= pivot) {
            low++;
        }
        // 交换low和high
        swap(arr, low, high);
    }
    // 还需要交换pivotIndex和low
    swap(arr, pivotIndex, low);
    // 最后返回low或high都可以
    return low;
}
private static void swap(int[] arr, int m, int n) {
    int temp = arr[m];
    arr[m] = arr[n];
    arr[n] = temp;
}

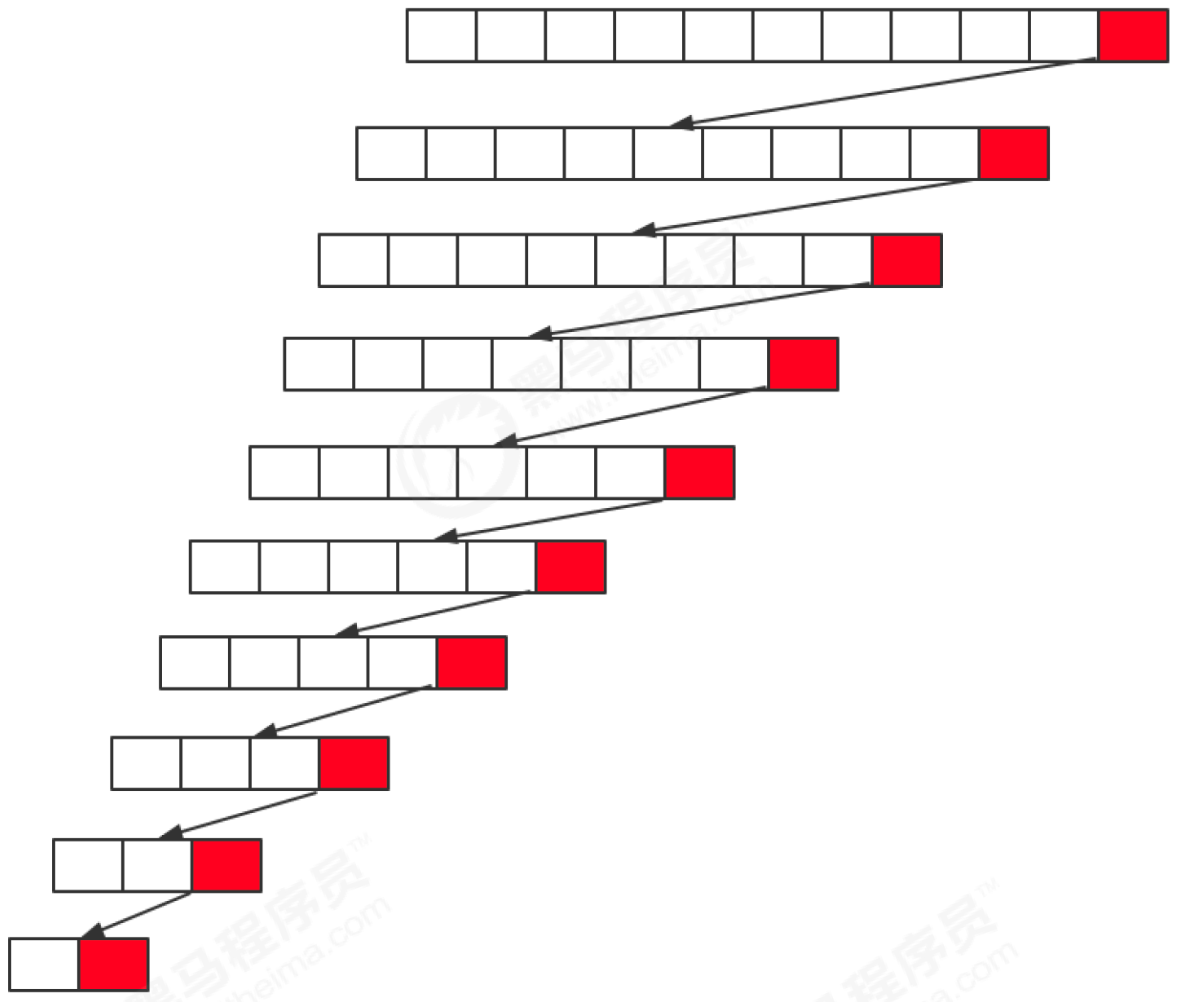
基本的快排实现，pivot 随机

「快速排序」在遇到特殊测试用例（「顺序数组」或者「逆序数组」）的时候，递归树会退化成链表，时间复杂度会变成 O(N^2)
代码

public static void quickSort(int[] arr) {
    // 边界判空
    if (arr == null || arr.length <= 1) {
        return;
    }
    quickSort(arr, 0, arr.length - 1);
}
private static void quickSort(int[] arr, int left, int right) {
    // 递归结束条件，如果不是>=而是>也是可以的，只是会多处一些无用的判断而已
    if (left >= right) {
        return;
    }
    // partition，将一个范围内的数组进行原地排序
    int partitionIndex = partition(arr, left, right);
    System.out.println("quickSort partitionIndex=" + partitionIndex + "，left=" + left + "，right=" + right);
    // 递归：将pivot左半边和右半部分都排序
    quickSort(arr, left, partitionIndex - 1);
    quickSort(arr, partitionIndex + 1, right);
}
private static int partition(int[] arr, int low, int high) {
    // 在[low,high]随机一个作为基准值
    int pivotIndex = low + new Random().nextInt(high - low) + 1;
    System.out.println("  -->> partition pivotIndex=" + pivotIndex + "，low=" + low + "，high=" + high);
    int pivot = arr[pivotIndex];
    // 将基准值和low交换，目前low作为基准值了
    swap(arr, pivotIndex, low);
    pivotIndex = low;
    // 将比pivot的小的放左边，比pivot大的放右边
    while (low < high) {
        // 一定要从high开始，否则会排序不对
        // 从high开始，往左找一个比pivot的小的值
        // 一定要小于等于，[0, 3, 3, 2, 6, 5, 8, 10, 2]，就会出现low=0,high=1，程序走不下去了
        while (low < high && arr[high] >= pivot) {
            high--;
        }
        // 从low开始，往右找一个比pivot的大的值
        while (low < high && arr[low] <= pivot) {
            low++;
        }
        // 交换low和high
        swap(arr, low, high);
    }
    // 还需要交换pivotIndex和low
    swap(arr, pivotIndex, low);
    // 最后返回low或high都可以
    return low;
}
private static void swap(int[] arr, int m, int n) {
    int temp = arr[m];
    arr[m] = arr[n];
    arr[n] = temp;
}

快速排序时间复杂度和稳定性

快速排序稳定性

快速排序是不稳定的算法，它不满足稳定算法的定义。

算法稳定性 – 假设在数列中存在 a[i]=a[j]，若在排序之前，a[i] 在 a[j] 前面；并且排序之后，a[i] 仍然在 a[j] 前面。则这个排序算法是稳定的！

快排为啥不是稳定的？

比如数组：{1,1,1,2,3,5,4}，pivot=1，一趟循环排序后 left=0,right=1，此时会进行交互，但这 2 个位置的元素都为 1，就打破了稳定性了。

快速排序的时间复杂度

快速排序的时间复杂度在最坏情况下是 O(N2)，平均的时间复杂度是 O(N*lgN)。

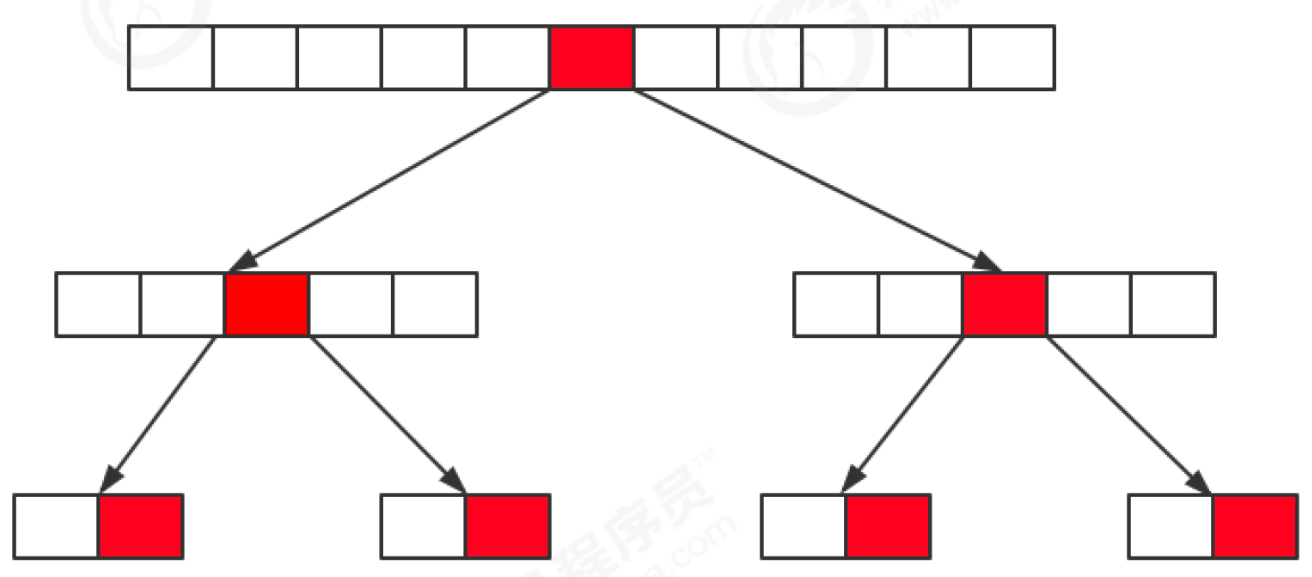
• 最优情况下快速排序的时间复杂度为**O(nlogn) **

每次都恰好五五分，一次递归共需比较 n 次，递归深度为 lg⁡n

为什么最少是 lg(N+1) 次? 快速排序是采用的分治法进行遍历的，我们将它看作一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的定义，它的深度至少是 lg(N+1)。因此，快速排序的遍历次数最少是 lg(N+1) 次。

• 最坏情况：每一次切分选择的基准数字是当前序列中最大数或者最小数，这使得每次切分都会有一个子组，那么总共就得切分 n 次，所以，最坏情况下，快速排序的时间复杂度为O(n^2)

快速排序的空间复杂度

快速排序只是使用数组原本的空间进行排序，所以所占用的空间应该是常量级的，但是由于每次划分之后是递归调用，所以递归调用在运行的过程中会消耗一定的空间，在一般情况下的空间复杂度为 O(logn)，在最差的情况下，若每次只完成了一个元素，那么空间复杂度为 O(n)。所以我们一般认为快速排序的空间复杂度为 O(logn)。

计数排序？ O(n)