01 数据结构和算法基础
数据结构基础
「数据结构」 指的是 数据的组织结构,用来组织、存储数据。数据结构可以分为 「逻辑结构」 和 「物理结构」。
- 逻辑结构可分为:集合结构、线性结构、树形结构、图形结构。
- 物理结构可分为:顺序存储结构、链式存储结构
作为线性表的两种存储方式 —— 链表和数组
数组
数组,所有元素都连续的存储于一段内存中,且每个元素占用的内存大小相同。这使得数组具备了通过下标快速访问数据的能力。
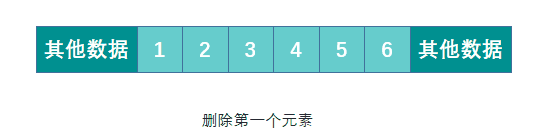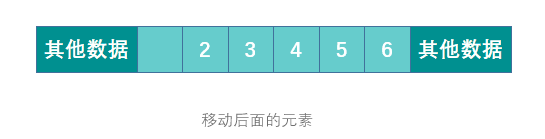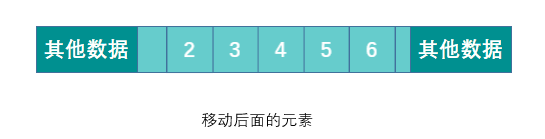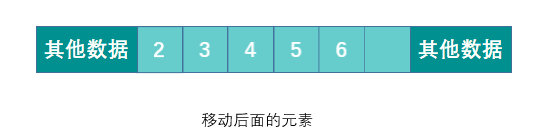
但连续存储的缺点也很明显,增加容量,增删元素的成本很高,时间复杂度均为 O(n)。
增加数组容量需要先申请一块新的内存,然后复制原有的元素。如果需要的话,可能还要删除原先的内存。
删除元素时需要移动被删除元素之后的所有元素以保证所有元素是连续的。增加元素时需要移动指定位置及之后的所有元素,然后将新增元素插入到指定位置,如果容量不足的话还需要先进行扩容操作。
总结一下数组的优缺点:
- 优点:可以根据偏移实现快速的随机读写。
- 缺点:扩容,增删元素极慢。
数组介绍
数组(Array):一种线性表数据结构。它使用一组连续的内存空间,来存储一组具有相同类型的数据。
数组是最基础、最简单的数据结构。数组是实现线性表的顺序结构存储的基础。它使用一组连续的内存空间,来存储一组具有相同类型的数据。
数组的最大特点的支持随机访问。其访问元素、改变元素的时间复杂度为 O(1),在尾部插入、删除元素的时间复杂度也是 O(1),普通情况下插入、删除元素的时间复杂度为 O(n)。
前缀和
前缀和就是提前将数组中前 n 个元素计算好存到一个临时的数组中去,prefix[i] 就代表着 nums[0..i-1] 所有元素的累加和,如果我们想求区间 nums[i..j] 的累加和,只要计算 prefix[j+1] - prefix[i] 即可,而不需要遍历整个区间求和。
前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和。
1
2
3
4
5
6
7
8
9
10
private int[] preSum;
public NumArray(int[] nums) {
if (nums.length <= 0) return;
// 前缀和:arrays数组中第i位置的值为前i个位置元素之和
preSum = new int[nums.length + 1];
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];
}
}
差分数组
前缀和 prefix[i] 就代表着 nums[0..i-1] 所有元素的累加和;diff[i] 就是 nums[i] 和 nums[i-1] 之差
差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
滑动窗口
什么是滑动窗口?
滑动窗口可用于解决一些字符串匹配问题。
典型的问题包括:在字符串 s 中找到一个最短的子串,使得其能覆盖到目标字符串 t。对于目标字符串 t,我们可以在字符串 s 上滑动窗口,当窗口包含 t 中的全部字符后,我们再根据题意考虑能否收缩窗口。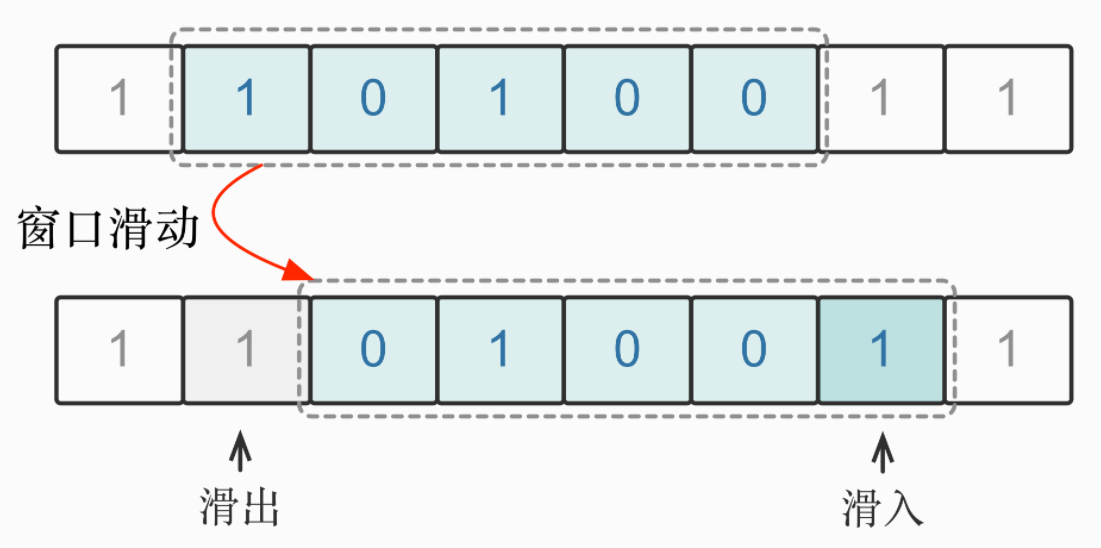
窗口的滑动过程可分解为以下两步基础操作:
- 窗口右边界往右滑动一位:窗口右端新加入一个字符,但窗口中的其他字符没有发生变化;
- 窗口左边界往右滑动一位:窗口左端滑出一个字符,但窗口中的其他字符没有发生变化
滑动窗口模板代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/* 滑动窗口算法框架 */
void slidingWindow(string s) {
unordered_map<char, int> window;
int left = 0, right = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}
滑动窗口模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
HashMap<Character, Integer> map;
int left = 0;
int right = 0;
while(right < t.length()) {
char ch = source[right];
window.put(ch, xxx)
right++;
// ... 进行窗口内数据的一系列更新
while( window需要缩小) {
char ch = source[left];
window.remove(ch);
left--;
// ... 进行窗口内数据的一系列更新
}
}
能否用滑动窗口?
1、什么时候应该扩大窗口?
2、什么时候应该缩小窗口?
3、什么时候更新答案?
二维数组技巧
矩阵翻转问题
原地矩阵对称转移公式
基础的对称操作,对于 NxN 的矩阵 matrix[i]j,各种对称的转移式如下:
- 上下对称:列不变,行对称,
matrix[i][j] = matrix[n-i-1][j] - 左右对称:行不变,列对称,
matrix[i][j] = matrix[i][n-j-1] - 主对角线对称:左上角到右下角的线,行列互换
matrix[i][j] = matrix[j][i] - 副对角线对称:左下角到右上角的线,
matrix[i][j] = matrix[n-j-1][n-i-1]
原地矩阵旋转多少度解题思路
以顺时针旋转 90° 为例: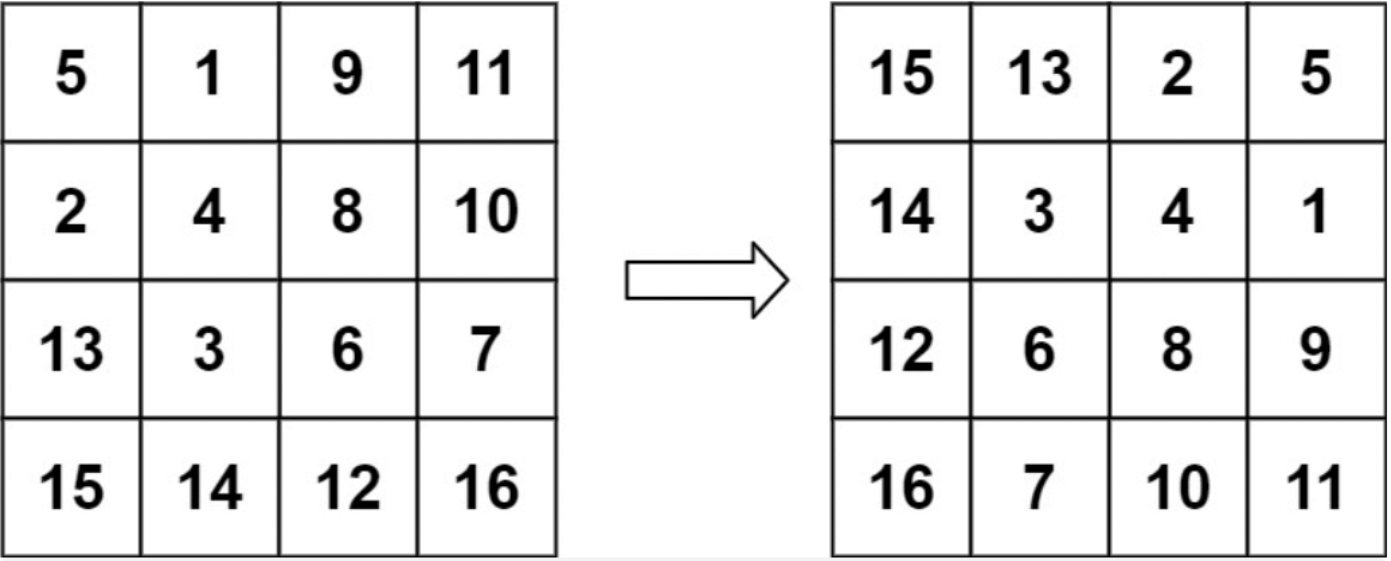
我们看最外层中间的元素,非四个角的元素,如 2;要将 2 从左图转换到右图,可以分 2 步骤进行
- 主对角线对称反转
matrix[i][j] = matrix[j][i] - 再左右对称反转
matrix[i][j] = matrix[i][n-j-1]
或者:
- 副对角线对称反转
matrix[i][j] = matrix[n-i-1][n-j-1] - 再上下对称反转
matrix[i][j] = matrix[n-i-1][j]
原地矩阵旋转多少度解题思路就是将旋转多少度分解成上述矩阵对称四种情况,然后套入公式即可。
原地矩阵旋转多少度示例
- 顺时针 90°
可以分解为:
主对角线对称→左右对称或上下对称→主对角线对称
- 顺时针 180° 旋转,可视为两次顺时针 90° 旋转:
顺时针 90° + 顺时针 90° = = 上下对称 + 主对角线对称 + 主对角线对称 + 左右对称 = 上下对称 + 左右对称 (主对角线对称抵消)
- 顺时针 270°,这个可以分解为:
顺时针 180° + 顺时针 90° = 左右对称 + 上下对称 + 上下对称 + 主对角线对称 = 左右对称 + 主对角线对称 (上下对称抵消)
- 逆时针 90° 旋转
左右对称 + 主对角线对称 或者 主对角线对称 + 上下对称。
算法
链表
链表,由若干个结点组成,每个结点包含数据域和指针域。结点结构如下图所示: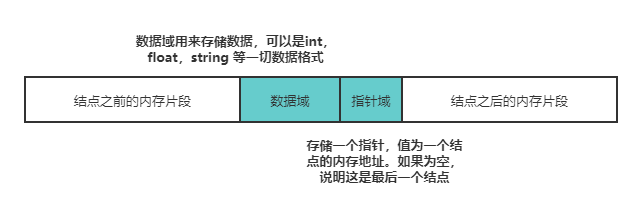
一般来讲,链表中只会有一个结点的指针域为空,该结点为尾结点,其他结点的指针域都会存储一个结点的内存地址。链表中也只会有一个结点的内存地址没有存储在其他结点的指针域,该结点称为头结点
「算法」 指的就是解决问题的方法。算法是一系列的运算步骤,这些运算步骤可以解决特定的问题。
算法拥有 5 个基本特性:输入、输出、有穷性、确定性、可行性。
算法复杂度
时间复杂度
算法复杂度(Algorithm complexity):在问题的输入规模为 n 的条件下,程序的时间使用情况和空间使用情况。
空间复杂度
时间复杂度(Time Complexity):在问题的输入规模为 n 的条件下,算法运行所需要花费的时间,可以记作为 T(n)。