文章

队列

发表于 更新于
作者 Hacket Zeng
39 分钟阅读
队列

队列介绍
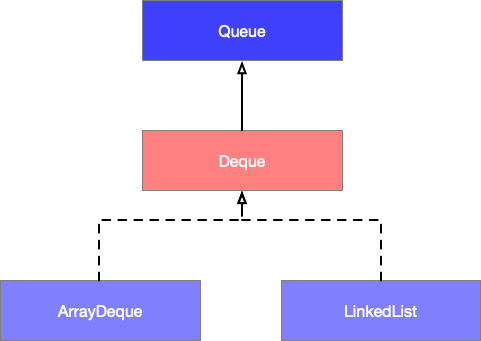
在 Java 中队列有两种形式，单向队列（ AbstractQueue ） 和 双端队列（ Deque ），单向队列效果如下所示，只能从一端进入，另外一端出去
qjp8z
双端队列（ Deque ）, Deque 是双端队列的线性数据结构, 可以在两端进行插入和删除操作，效果如下所示：

Queue 单向队列

Queue 概述

队列是一种特殊的线性表，它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列中没有元素时，称为空队列。
在队列这种数据结构中，最先插入的元素将是最先被删除的元素；反之最后插入的元素将是最后被删除的元素，因此队列又称为 “ 先进先出 “（FIFO—first in first out）的线性表。
Queue 定义了三组方法

操作抛出异常返回特殊值说明
插入add(e)offer(e)插入到队列中
移除remove()poll()返回队列的 head，并移除 head，poll() 如果队列为空返回 null
检查element()peek()返回队列的 head，不移除 head，peek() 如果队列为空返回 null

Queue 特点

任何一个 Queue 实现者都应该指定排序属性；
Queue 接口没有定义阻塞队列的方法，定义在 BlockingQueue 接口；
Queue 的实现者通常不允许插入 null 元素 (LinkedList 除外)

阻塞和非阻塞 Queue

Java 提供的线程安全的 Queue 可以分为阻塞队列和非阻塞队列；阻塞队列的典型例子是 BlockingQueue，非阻塞队列典型例子是 ConcurrentLinkedQueue。
阻塞队列 -BlockingQueue
见 BlockingQueue阻塞队列 章节

Deque 双向队列

双向队列 (Deque) 是 Queue 的一个子接口，双向队列是指该队列两端的元素既能入队 (offer) 也能出队 (poll),如果将 Deque 限制为只能从一端入队和出队，则可实现栈的数据结构。对于栈而言，有入栈 (push) 和出栈 (pop)，遵循先进后出原则。
双端队列（ Deque ）的子类分别是 ArrayDeque 和 LinkedList，ArrayDeque 基于数组实现的双端队列，而 LinkedList 基于双向链表实现的双端队列，它们的继承关系如下图所示：
9p8lg
接口 Deque 和 Queue 提供了两套 API ，存在两种形式，分别为抛出异常，和不抛出异常，返回一个特殊值 null 或者布尔值 ( true		false )。
操作类型抛出异常返回特殊值
插入addXXX(e)offerXXX(e)
移除removeXXX()pollXXX()
查找element()peekXXX()

ArrayDeque

ArrayDeque 是基于（循环）数组的方式实现双端队列，数组初始化容量为 16（JDK 8），结构图如下所示。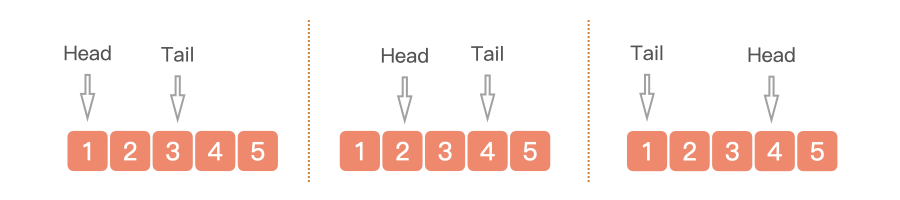
pncm1
ArrayDeque 具有以下特点：

  • 因为双端队列只能在头部和尾部插入或者删除元素，所以时间复杂度为 O(1)，但是在扩容的时候需要批量移动元素，其时间复杂度为 O(n)
  • 扩容的时候，将数组长度扩容为原来的 2 倍，即 n « 1
  • 数组采用连续的内存地址空间，所以查询的时候，时间复杂度为 O(1)
  • 它是非线程安全的集合

LinkedList

LinkedList 基于双向链表实现的双端队列，它的结构图如下所示。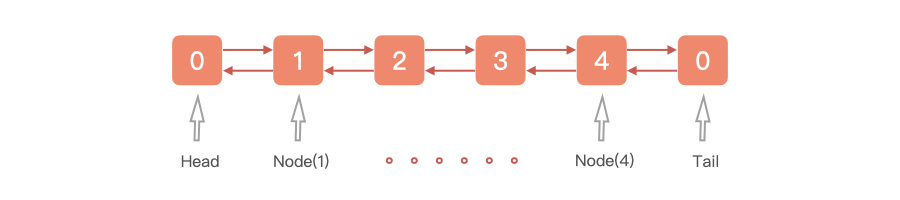
ms74f
LinkedList 特点：

  • LinkedList 是基于双向链表的结构来存储元素，所以长度没有限制，因此不存在扩容机制
  • 由于链表的内存地址是非连续的，所以只能从头部或者尾部查找元素，查询的时间复杂为 O(n)，但是 JDK 对 LinkedList 做了查找优化，当我们查找某个元素时，若 index < (size / 2)，则从 head 往后查找，否则从 tail 开始往前查找 , 但是我们在计算时间复杂度的时候，常数项可以省略，故时间复杂度 O(n)
1
2
3
4
5
6
7
8

Node<E> node(int index) {
    // size >> 1 等价于 size / 2
    if (index < (size >> 1)) {
        // form head to tail
    } else {
        // form tail to head
    }
}
  • 链表通过指针去访问各个元素，所以插入、删除元素只需要更改指针指向即可，因此插入、删除的时间复杂度 O(1)
  • 它是非线程安全的集合

ArrayDeque 和 LinkedList

ArrayDeque 和 LinkedList 对比

ArrayDeque 和 LinkedList 的特点如下所示：

集合类型数据结构初始化及扩容插入/删除时间复杂度查询时间复杂度是否是线程安全
ArrqyDeque循环数组初始化：16
扩容：2 倍		0(n)0(1)否
LinkedList双向链表无0(1)0(n)否

不用 LinkedList，用 ArrayDequeue 替换？

从速度的角度

ArrayDeque 基于数组实现双端队列，而 LinkedList 基于双向链表实现双端队列，数组采用连续的内存地址空间，通过下标索引访问，链表是非连续的内存地址空间，通过指针访问，所以在寻址方面数组的效率高于链表。

CPU 缓存对数组友好而对链表不友好。

” 数组简单易用，在实现上使用的是连续的内存空间，可以借助 CPU 的缓存机制，预读数组中的数据，所以访问效率越高。而链表在内存中并不是连续存储，所以对 CPU 缓存不友好，没有办法预读。”

原因: CPU 读取内存的时候，会把一片连续的内存块读取出来，然后放到缓存中。因为数组结构是连续的内存地址，所以数组全部或者部分元素被连续存在 CPU 缓存里面，cpu 读取缓存里面的每个元素的时间平均只要 3 个 CPU 时钟周期。而链表的节点是分散在堆空间（内存）里面的，cpu 需要去读取内存，平均读取时间需要 100 个 CPU 时钟周期。

所以 cpu 访问数组比链表快了大约 33 倍！

从内存的角度

虽然 LinkedList 没有扩容的问题，但是插入元素的时候，需要创建一个 Node 对象, 换句话说每次都要执行 new 操作，当执行 new 操作的时候，其过程是非常慢的，会经历两个过程：类加载过程 、对象创建过程。

  • 类加载过程
    • 会先判断这个类是否已经初始化，如果没有初始化，会执行类的加载过程
    • 类的加载过程：加载、验证、准备、解析、初始化等等阶段，之后会执行 <clinit>() 方法，初始化静态变量，执行静态代码块等等
  • 对象创建过程
    • 如果类已经初始化了，直接执行对象的创建过程
    • 对象的创建过程：在堆内存中开辟一块空间，给开辟空间分配一个地址，之后执行初始化，会执行 <init>() 方法，初始化普通变量，调用普通代码块

ArrayDeque

ArrayDeque 源码

1
2
3
4
5
6
7

public class ArrayDeque<E> extends AbstractCollection<E> implements Deque<E> {
	transient Object[] elements; // 数组的长度，总是 2 的整数次幂
    transient int head; // 头指针，表示队首元素所在位置
    transient int tail; // 尾指针，表示队尾元素所在位置
    // 最小初始化容量是 8（JDK 8）， 这是为了保证初始容量都是 2 的整数次幂, 减少计算步骤
    private static final int MIN_INITIAL_CAPACITY = 8;
}

构造函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

public ArrayDeque() {
    elements = new Object[16];
}
public ArrayDeque(int numElements) {
    allocateElements(numElements);
}
// 计算数组的大小，返回值是最接近 2 的整数次幂
private void allocateElements(int numElements) {
    int initialCapacity = MIN_INITIAL_CAPACITY; // 最小初始化容量是 8（JDK 8）
    // Find the best power of two to hold elements.
    // Tests "<=" because arrays aren't kept full.
    if (numElements >= initialCapacity) {
        // 大于或者等于初始化容量时
        // 会调整为最接近 2 的整数次幂，例如 9 -> 16
        initialCapacity = numElements;
        initialCapacity |= (initialCapacity >>>  1);
        initialCapacity |= (initialCapacity >>>  2);
        initialCapacity |= (initialCapacity >>>  4);
        initialCapacity |= (initialCapacity >>>  8);
        initialCapacity |= (initialCapacity >>> 16);
        initialCapacity++;

        // 当传人值非常大，经过计算变成负数，会重新初始化为 2 ^ 30
        if (initialCapacity < 0)   // Too many elements, must back off
            initialCapacity >>>= 1;// Good luck allocating 2 ^ 30 elements
    }
    elements = new Object[initialCapacity];
}
  • 无参构造方法（默认），直接初始化容量为 16 的数组
  • 有参构造方法，会初始化最接近 2 的整数次幂的大小的数组。而 allocateElements(numElements) 方法的返回值是最接近 2 的整数次幂

计算任意一个数接近 2 的整数次幂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

private static int allocateElements(int numElements) {
    int initialCapacity = MIN_INITIAL_CAPACITY;
    // Find the best power of two to hold elements.
    // Tests "<=" because arrays aren't kept full.
    if (numElements >= initialCapacity) {
        initialCapacity = numElements;
        initialCapacity |= (initialCapacity >>> 1);
        initialCapacity |= (initialCapacity >>> 2);
        initialCapacity |= (initialCapacity >>> 4);
        initialCapacity |= (initialCapacity >>> 8);
        initialCapacity |= (initialCapacity >>> 16);
        initialCapacity++;

        if (initialCapacity < 0)   // Too many elements, must back off
            initialCapacity >>>= 1;// Good luck allocating 2 ^ 30 elements
    }
    return initialCapacity;
}

如果 initialCapacity=8：

i=0, initialCapacity=8 // … 中间都是 8 i=7, initialCapacity=8 i=8, initialCapacity=16 // … 中间都是 16 i=15, initialCapacity=16 i=16, initialCapacity=32 i=17, initialCapacity=32 i=18, initialCapacity=32 i=19, initialCapacity=32

ArrayDeque 的 2 的整数次幂计算逻辑，相比于 HashMap 的计算逻辑是有一点区别的，如下图所示。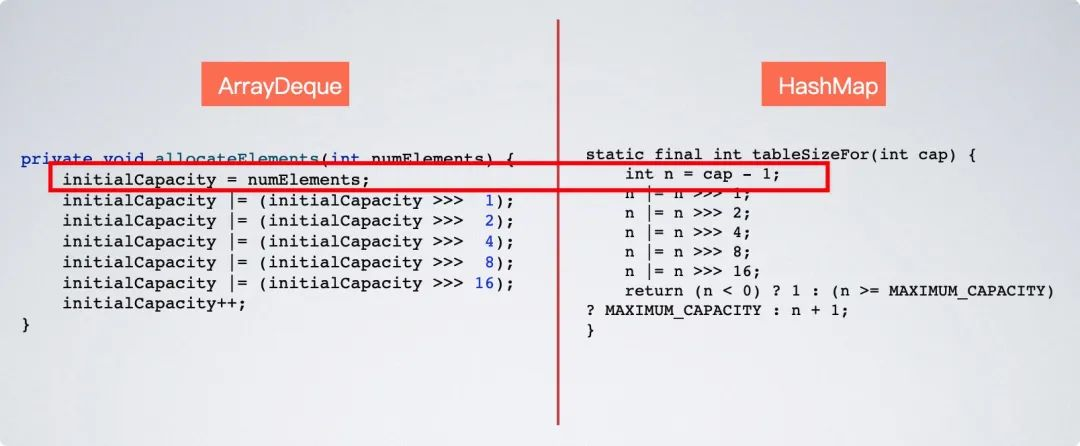
qtsw1
HashMap 的 2 的整数次幂计算逻辑，在进行位运算之前先执行了 cap - 1 的操作，而 ArrayDeque 没有，这么做的区别在于，假设传进去来的是 8 正好是 2 的整数次幂， ArrayDeque 计算出来的结果是 16，而 HashMap 的计算结果是其本身 8 ，这么做的目的，是为了省内存。

i=0, initialCapacity(ArrayDeque)=8, initialCapacity(HashMap)=8 i=1, initialCapacity(ArrayDeque)=8, initialCapacity(HashMap)=8 i=2, initialCapacity(ArrayDeque)=8, initialCapacity(HashMap)=8 i=3, initialCapacity(ArrayDeque)=8, initialCapacity(HashMap)=8 i=4, initialCapacity(ArrayDeque)=8, initialCapacity(HashMap)=8 i=5, initialCapacity(ArrayDeque)=8, initialCapacity(HashMap)=8 i=6, initialCapacity(ArrayDeque)=8, initialCapacity(HashMap)=8 i=7, initialCapacity(ArrayDeque)=8, initialCapacity(HashMap)=8 i=8, initialCapacity(ArrayDeque)=16, initialCapacity(HashMap)=8 i=9, initialCapacity(ArrayDeque)=16, initialCapacity(HashMap)=16 i=10, initialCapacity(ArrayDeque)=16, initialCapacity(HashMap)=16 i=11, initialCapacity(ArrayDeque)=16, initialCapacity(HashMap)=16 i=12, initialCapacity(ArrayDeque)=16, initialCapacity(HashMap)=16 i=13, initialCapacity(ArrayDeque)=16, initialCapacity(HashMap)=16 i=14, initialCapacity(ArrayDeque)=16, initialCapacity(HashMap)=16 i=15, initialCapacity(ArrayDeque)=16, initialCapacity(HashMap)=16 i=16, initialCapacity(ArrayDeque)=32, initialCapacity(HashMap)=16 i=17, initialCapacity(ArrayDeque)=32, initialCapacity(HashMap)=32 i=18, initialCapacity(ArrayDeque)=32, initialCapacity(HashMap)=32 i=19, initialCapacity(ArrayDeque)=32, initialCapacity(HashMap)=32

为什么要设置成 2 的整数次幂？

任何一个数 和 2^n -1 做与运算，保证指针 head 的索引和尾指针 tail 的索引，落在队列范围内。

  • 任意 1 个数和 2^n 做与运算，值为 0 或 2^n
  • 任意 1 个数和 2^n - 1 做与运算，值在 [0, 2^n - 1] 之间
1
2
3

private static int xxx(int n, int len) {
    return n & (len - 1);
}

len=8，对应的二进制为：00000000 00000000 00000000 00001000

任意数 n，n&8 做与运算，计算的值要么是 8，要么是 0

len-1=7，对应的二进制为：00000000 00000000 00000000 00000111

任意数 n，n&7 做与运算，计算的值都是在 [0, 7] 之间

入队列

无论是通过 add(e) 或者 offer(e) 方法将元素插入到队列中。最终都是调用 addLast(E e) 方法

1
2
3
4
5
6
7

public void addLast(E e) {
    if (e == null)
        throw new NullPointerException("e == null");
    elements[tail] = e;
    if ( (tail = (tail + 1) & (elements.length - 1)) == head) 
        doubleCapacity(); // 扩容为两倍，通过数组拷贝的方式进行扩容
}

循环队列

实现循环队列，最核心的就是下面这句：

1

tail = (tail + 1) & (elements.length - 1)) == head
  • 重新计算 tail 的索引指向的下一个位置
  • 判断队列是否已满，如果已满执行 doubleCapacity() 方法进行扩容

PriorityQueue 优先级队列

什么是 PriorityQueue？

PriorityQueue 类在 Java1.5 中引入。PriorityQueue，即优先队列。优先队列的作用是能保证每次取出的元素都是队列中权值最小的（Java 的优先队列每次取最小元素，C++ 的优先队列每次取最大元素）。这里牵涉到了大小关系，元素大小的评判可以通过元素本身的自然顺序（natural ordering），也可以通过构造时传入的比较器（Comparator，类似于 C++ 的仿函数）。

PriorityQueue 特性

  1. 默认小顶堆，无界的，非阻塞，线程不安全的
  2. 放入的元素需实现 Comparable 接口；如果元素未实现 Comparable，也可以在 PriorityQueue 传入 Comparator 接口
  3. Java 中 PriorityQueue 实现了 Queue 接口，不允许放入 null 元素
  4. 存储的结构是数组，数据结构为完全二叉树 (二叉堆)

PriorityQueue 原理

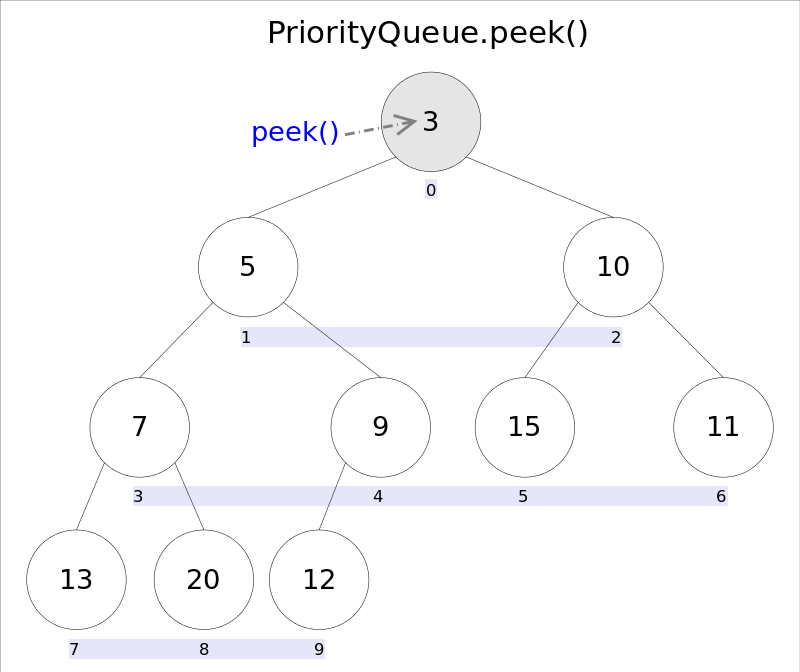
通过堆实现，具体说是通过完全二叉树（complete binary tree）实现的小顶堆（任意一个非叶子节点的权值，都不大于其左右子节点的权值），也就意味着可以通过数组来作为 PriorityQueue 的底层实现。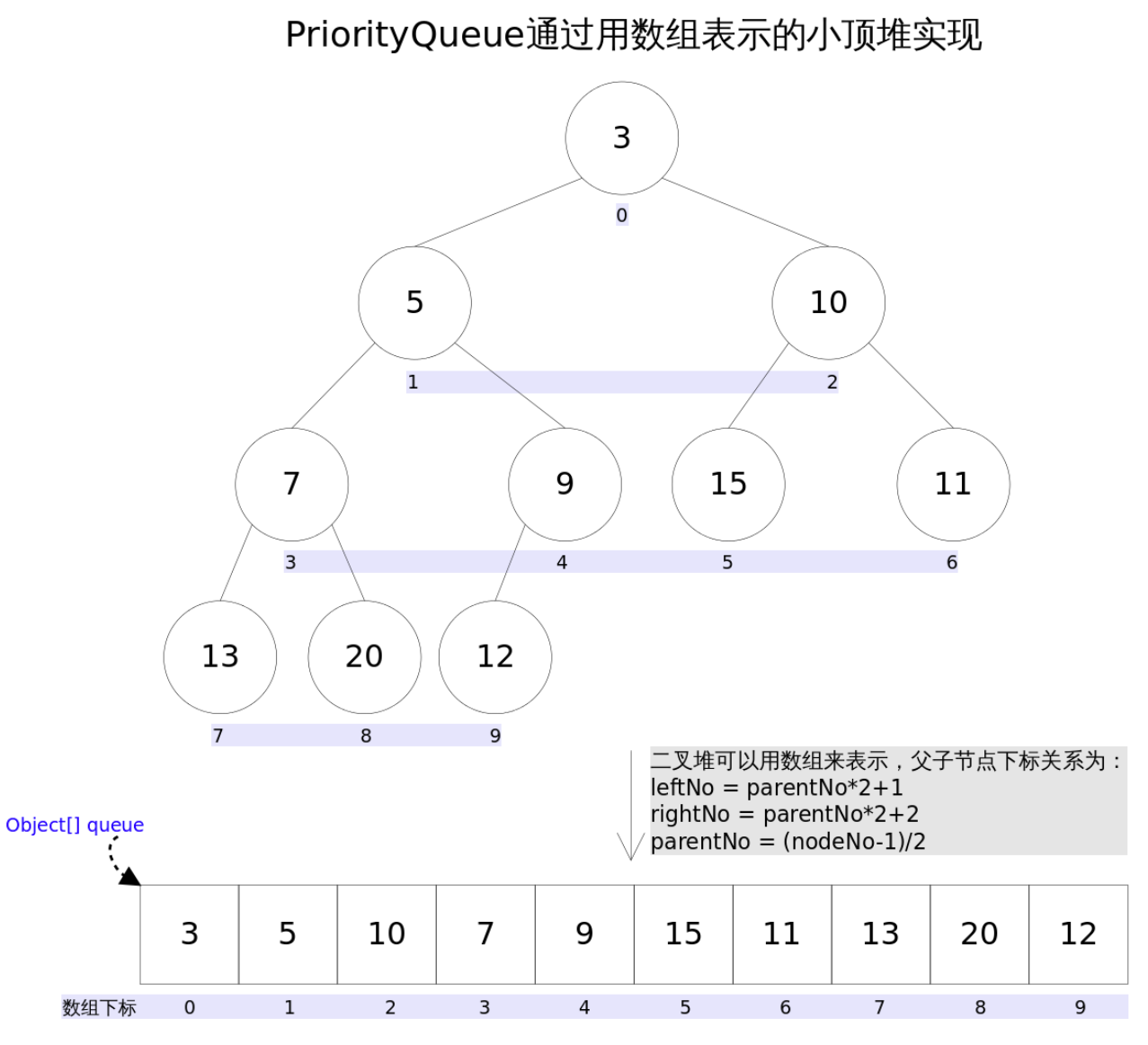
1retg
上图中我们给每个元素按照层序遍历的方式进行了编号，如果你足够细心，会发现父节点和子节点的编号是有联系的，更确切的说父子节点的编号之间有如下关系：

1
2
3

leftNo(左子节点) = parentNo*2+1
rightNo(右子节点) = parentNo*2+2
parentNo((父节点)) = (nodeNo-1)/2

通过上述三个公式，可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储堆的原因。

PriorityQueue 的 peek() 和 element() 操作是常数时间；add(), offer(),无参数的 remove() 以及 poll() 方法的时间复杂度都是 log(N)。

add()/offer() 添加元素

add(E e) 和 offer(E e) 的语义相同，都是向优先队列中插入元素，只是 Queue 接口规定二者对插入失败时的处理不同，前者在插入失败时抛出异常，后则则会返回 false。对于 PriorityQueue 这两个方法其实没什么差别。
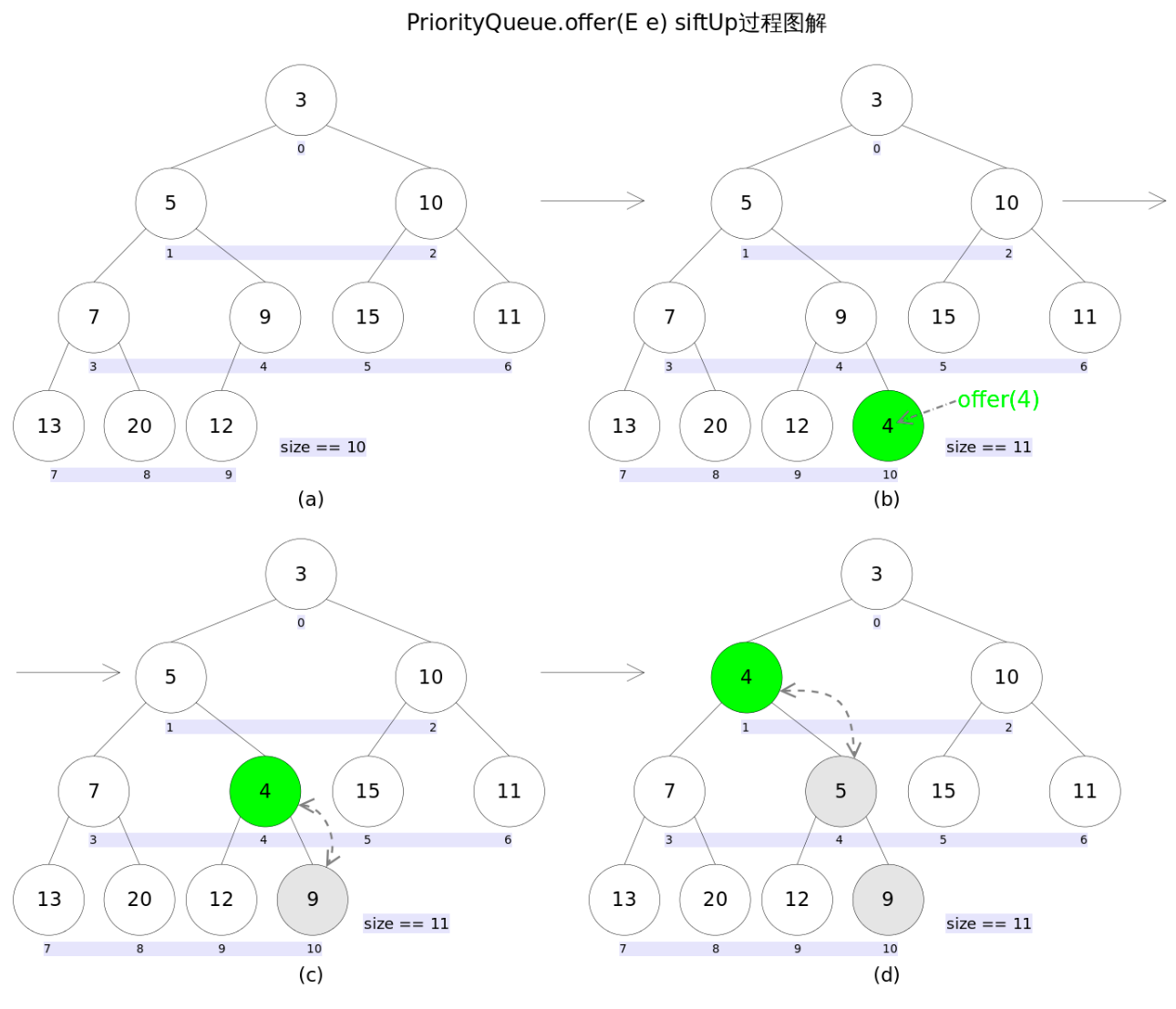
新加入的元素可能会破坏小顶堆的性质，因此需要进行必要的调整。
54vgt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

// PriorityQueue
public boolean add(E e) {
    return offer(e);
}
public boolean offer(E e) {
    if (e == null) // 不允许放入null元素
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
        grow(i + 1); // 自动扩容
    size = i + 1;
    if (i == 0) // 队列原来为空，这是插入的第一个元素
        queue[0] = e;
    else
        siftUp(i, e); // 上浮调整
    return true;
}

扩容函数 grow() 类似于 ArrayList 里的 grow() 函数，就是再申请一个更大的数组，并将原数组的元素复制过去：

1
2
3
4
5
6
7
8
9
10
11

private void grow(int minCapacity) {
    int oldCapacity = queue.length;
    // Double size if small; else grow by 50%
    int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                     (oldCapacity + 2) :
                                     (oldCapacity >> 1));
    // overflow-conscious code
    if (newCapacity - MAX_ARRAY_SIZE > 0)
        newCapacity = hugeCapacity(minCapacity);
    queue = Arrays.copyOf(queue, newCapacity);
}

siftUp(int k, E x) 方法，该方法用于插入元素 x 并维持堆的特性：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

private void siftUp(int k, E x) {
    if (comparator != null)
        siftUpUsingComparator(k, x);
    else
        siftUpComparable(k, x);
}
private void siftUpUsingComparator(int k, E x) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (comparator.compare(x, (E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}
private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
        // 获取父节点的下标
        int parent = (k - 1) >>> 1;
        // 父节点的元素值
        Object e = queue[parent];
        // 如果新插入的元素比父节点的元素值大，循环结束，新插入节点直接插入最后即可
        if (key.compareTo((E) e) >= 0)
            break;
        // 否则需要把父节点元素值放到新插入节点的下标（可以理解为父节点与新插入元素调换位置）
        queue[k] = e;
        // 重复进行，知道父节点比子节点小
        k = parent;
    }
    // 新插入元素放入排序后的下标
    queue[k] = key;
}

从 k 指定的位置开始，将 x 逐层与当前点的 parent 进行比较并交换，直到满足 x >= queue[parent] 为止

element() 和 peek() 获取堆顶元素（不删除）

1
2
3
4
5
6
7
8
9
10

public E peek() {
    return (size == 0) ? null : (E) queue[0]; // 0下标处的那个元素就是最小的那个
}
public E element() {
    E x = peek();
    if (x != null)
        return x;
    else
        throw new NoSuchElementException();
}
  1. 直接返回数组 0 下标处的那个元素即可，堆顶的最小值
  2. element() 和 peek() 的语义完全相同，都是获取但不删除队首元素，也就是队列中权值最小的那个元素
  3. 二者唯一的区别是当方法失败时 element() 抛出异常，peek() 返回 null

exxp4

remove() 和 poll()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0];
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
        siftDown(0, x); // 从k指定的位置开始，将x逐层向下与当前点的左右孩子中较小的那个交换，直到x小于或等于左右孩子中的任何一个为止。
    return result;
}
public E remove() {
    E x = poll();
    if (x != null)
        return x;
    else
        throw new NoSuchElementException();
}

remove() 和 poll() 方法的语义也完全相同，都是获取并删除队首元素，区别是当方法失败时前者抛出异常，后者返回 null

由于删除操作会改变队列的结构，为维护小顶堆的性质，需要进行必要的调整。
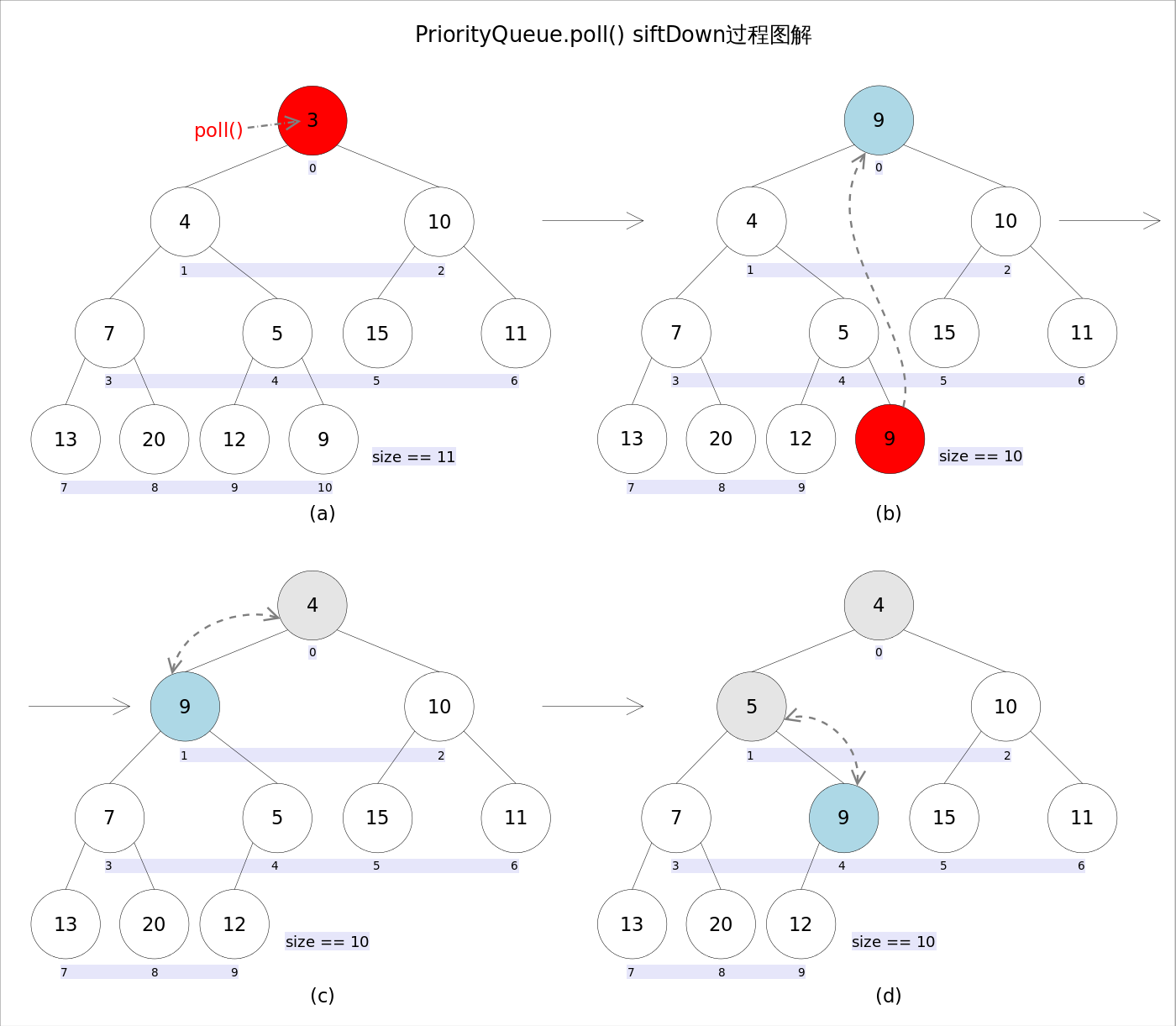
85bkg

remove(Object o)

用于删除队列中跟 o 相等的某一个元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

public boolean remove(Object o) {
    int i = indexOf(o);
    if (i == -1)
        return false;
    else {
        removeAt(i);
        return true;
    }
}
E removeAt(int i) {
    // assert i >= 0 && i < size;
    modCount++;
    int s = --size;
    if (s == i) // removed last element
        queue[i] = null;
    else {
        E moved = (E) queue[s];
        queue[s] = null;
        siftDown(i, moved);
        if (queue[i] == moved) {
            siftUp(i, moved);
            if (queue[i] != moved)
                return moved;
        }
    }
    return null;
}

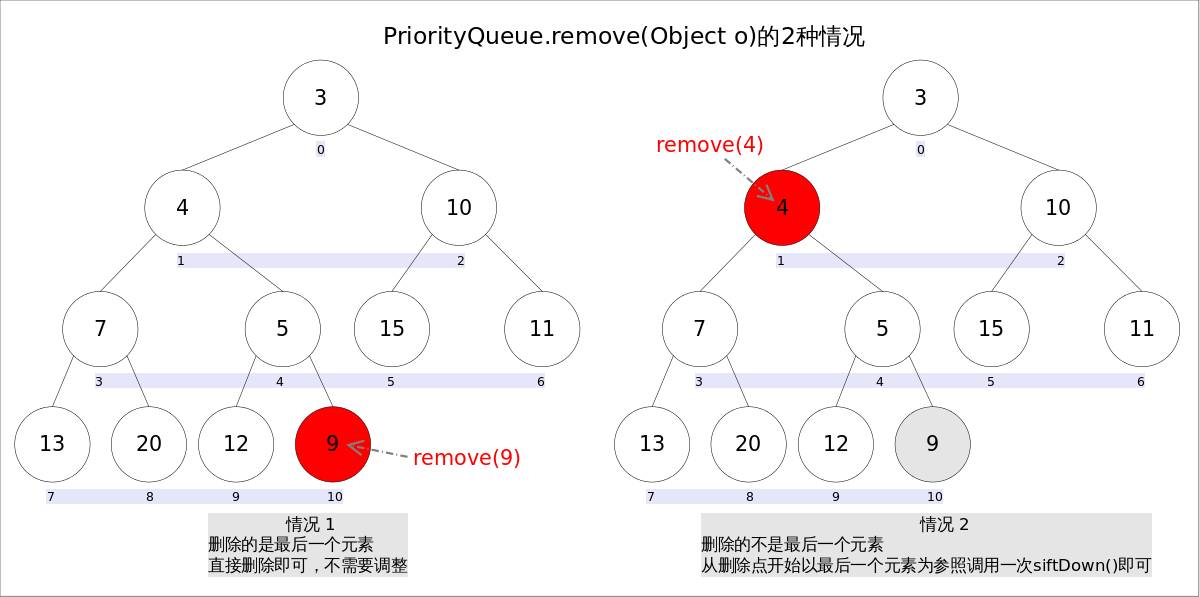
由于删除操作会改变队列结构，所以要进行调整；又由于删除元素的位置可能是任意的，所以调整过程比其它函数稍加繁琐。具体来说，remove(Object o) 可以分为 2 种情况：

  1. 删除的是最后一个元素。直接删除即可，不需要调整。
  2. 删除的不是最后一个元素，从删除点开始以最后一个元素为参照调用一次 siftDown() 即可。

5fut5

测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

public class 优先队列测试 {

    public static void main(String[] args) {
//        test1();
        test2();
    }

    private static void test2() {
        PriorityQueue<String> pq = new PriorityQueue<>(new Comparator<String>() {
            @Override
            public int compare(String s, String s1) { // s待插入元素，s1已经插入元素
                // s1.compareTo(s); 降序
                // s.compareTo(s1); 升序
                int c = s1.compareTo(s);
                System.out.println("s=" + s + ",s1=" + s1 + ",c=" + c);
                return c;

            }
        });
        pq.add("a");
        pq.add("c");
        pq.add("d");
        pq.add("e");
        pq.add("z");
        pq.add("1");
        pq.add("2");
        System.out.println(pq);
        while (!pq.isEmpty()) {
            String val = pq.poll();
            System.out.println(val);
        }
        // 输出 zedca21
    }

    /**
     * 自然排序: 升序
     */
    private static void test1() {
        PriorityQueue<String> pq = new PriorityQueue<>();
        pq.add("a");
        pq.add("c");
        pq.add("d");
        pq.add("e");
        pq.add("z");
        pq.add("1");
        pq.add("2");
        System.out.println(pq);
        while (!pq.isEmpty()) {
            String val = pq.poll();
            System.out.println(val);
        }
        // 输出 12acdez
    }
    
    public static void main(String[] args) {
        int[] a = {2000, 10};
        int[] a0 = {200, 1};
        int[] a1 = {300, 2};
        int[] a2 = {400, 6};
        int[] a3 = {400, 4};
        int[] a4 = {1000, 3};
        PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>() {
            @Override
            public int compare(int[] arr1, int[] arr2) {
                int c = arr2[0] != arr1[0] ? arr2[0] - arr1[0] : arr2[1] - arr1[1];
//                System.out.println("arr1=" + Arrays.toString(arr1) + ",arr2=" + Arrays.toString(arr2) + ",c=" + c);
                return c;
            }
        });
        pq.add(a);
        pq.add(a0);
        pq.add(a1);
        pq.add(a2);
        pq.add(a3);
        pq.add(a4);
        while (!pq.isEmpty()) {
            System.out.print(Arrays.toString(pq.poll()) + ", ");
        }
    }
    // 输出： [2000, 10], [1000, 3], [400, 6], [400, 4], [300, 2], [200, 1], 
}

PriorityQueue 应用

解决 top k 问题

BlockingQueue 阻塞队列

BlockingQueue 概述

BlockingQueue，顾名思义，” 阻塞队列 “：可以提供阻塞功能的队列。BlockingQueue，顾名思义，” 阻塞队列 “：可以提供阻塞功能的队列。首先，看看 BlockingQueue 提供的常用方法：

 可能报异常返回布尔值可能阻塞设定等待时间
入队add(e)offer(e)put(e)offer(e, timeout, unit)
出队remove()poll()take()poll(timeout, unit)
查看element()peek()无无
  • add()、remove()、element() 方法不会阻塞线程。当不满足约束条件时，会抛出 IllegalStateException 异常。例如：当队列被元素填满后，再调用 add(e)，则会抛出异常。
  • offer(e) poll() peek() 方法也不会阻塞线程，也不会抛出异常。例如：当队列被元素填满后，再调用 offer(e)，则不会插入元素，函数返回 false。
  • 要想要实现阻塞功能，需要调用 put(e) take() 方法。当不满足约束条件时，会阻塞线程。

BlockingQueue 特点

  • 线程安全的
  • 不能插入 null 值

阻塞的主要问题是进行线程阻塞和唤醒带来的性能问题，属于一种悲观策略。非阻塞版本是一种基于冲突检测的乐观策略。

具体实现类

LinkedBlockingQueue

若其构造函数带一个规定大小的参数，生成的 BlockingQueue 有大小限制，若不带大小参数，所生成的 BlockingQueue 的大小由 Integer.MAX_VALUE 来决定；底层由链表实现。所含对象以 FIFO 顺序排序的。

PriorityBlockingQueue

一个支持优先级排序的无界阻塞队列；
其所含对象的排序不是 FIFO,而是依据对象的自然排序顺序或者是构造函数的 Comparator 决定的顺序。

ArrayBlockingQueue

一个由数组结构组成的有界阻塞队列；
其构造函数必须带一个 int 参数来指明其大小，底层是数组结构，使用一把锁，性能相对列表的稍慢，但是在加入和移出过程中不需要生产 node，固在大量数据的情况下 gc 有优势。所含对象以 FIFO 顺序排序的。

PriorityBlockingQueue 优先级阻塞队列

什么是 PriorityBlockingQueue？

PriorityBlockingQueue 是一个支持优先级的无界阻塞队列，直到系统资源耗尽。默认情况下元素采用自然顺序升序排列。也可以自定义类实现 compareTo() 方法来指定元素排序规则，或者初始化 PriorityBlockingQueue 时，指定构造参数 Comparator 来对元素进行排序。但需要注意的是不能保证同优先级元素的顺序。PriorityBlockingQueue 也是基于最小二叉堆实现，使用基于 CAS 实现的自旋锁来控制队列的动态扩容，保证了扩容操作不会阻塞 take 操作的执行

PriorityBlockingQueue 使用

PriorityBlockingQueue 有四个构造方法

  1. public PriorityBlockingQueue()
  2. public PriorityBlockingQueue(int initialCapacity)//
    根据 initialCapacity 来设置队列的初始容量
  3. public PriorityBlockingQueue(int initialCapacity, Comparator<? super<br>E> comparator) // 根据 initialCapacity 来设置队列的初始容量，并根据 comparator 对象来对数据进行排序
  4. public PriorityBlockingQueue(Collection<? extends E> c) // 根据集合来创建队列

常用的添加元素函数

  1. add()：若超出了度列的长度会直接抛出异常：
  2. put()：若向队尾添加元素的时候发现队列已经满了会发生阻塞一直等待空间，以加入元素。
  3. offer()：如果发现队列已满无法添加的话，会直接返回 false。

从队列中取出并移除头元素的方法

  1. poll()：若队列为空，返回 null。
  2. remove()：若队列为空，抛出 NoSuchElementException 异常。
  3. take()：若队列为空，发生阻塞，等待有元素。

返回队列头列表

  1. element()：返回队列头元素，如果为空则抛出异常 NoSuchEleMentException
  2. peek()：返回队列头元素，如果为空则返回 null

案例

生产者消费者

1 个生产者生成数据，1 个消费者消费数据，高优先级的数据先处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

public class PriorityBlockingQueue优先阻塞队列测试 {

    private static class MyTask implements Comparable<MyTask> {
        public int priority = 0;
        public String taskName;

        @Override
        public int compareTo(MyTask o) { // 大于0，则优先级高，小于0，则优先级低
            if (o.priority > this.priority) {
                return 1;
            }
            return -1;
        }
    }

    public static void main(String[] args) {
        PriorityBlockingQueue<MyTask> queue = new PriorityBlockingQueue<>();

        new Thread("Thread-生产者-->>") {
            @Override
            public void run() {
                super.run();
                Random random = new Random();
                // 往队列中放是个任务，从TaskName是按照顺序放进去的，优先级是随机的
                for (int i = 1; i < 20; i++) {
                    MyTask task = new MyTask();
                    task.priority = random.nextInt(20);
                    task.taskName = "taskName" + i;
                    queue.offer(task);
                    System.out.println("[" + Thread.currentThread().getName() + "]" + "生产了任务：" + task.taskName + "，优先级是：" + task.priority);
                    try {
                        Thread.sleep(1000L);
                    } catch (InterruptedException e) {
                        e.printStackTrace();
                    }
                }
            }
        }.start();

        new Thread("<<--Thread-消费者") {
            @Override
            public void run() {
                while (isAlive()) {
                    try {
                        MyTask task = queue.take();
                        System.out.println("[" + Thread.currentThread().getName() + "]" + "消费了任务：" + task.taskName + "，优先级是：" + task.priority);
                        Thread.sleep(5000L);
                    } catch (InterruptedException e) {
                        e.printStackTrace();
                    }
                }
            }
        }.start();
    }
}

输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

[Thread-生产者-->>]生产了任务：taskName1，优先级是：9
[<<--Thread-消费者]消费了任务：taskName1，优先级是：9
[Thread-生产者-->>]生产了任务：taskName2，优先级是：12
[Thread-生产者-->>]生产了任务：taskName3，优先级是：11
[Thread-生产者-->>]生产了任务：taskName4，优先级是：11
[Thread-生产者-->>]生产了任务：taskName5，优先级是：19
[<<--Thread-消费者]消费了任务：taskName5，优先级是：19
[Thread-生产者-->>]生产了任务：taskName6，优先级是：16
[Thread-生产者-->>]生产了任务：taskName7，优先级是：7
[Thread-生产者-->>]生产了任务：taskName8，优先级是：8
[Thread-生产者-->>]生产了任务：taskName9，优先级是：15
[Thread-生产者-->>]生产了任务：taskName10，优先级是：17
[<<--Thread-消费者]消费了任务：taskName10，优先级是：17
[Thread-生产者-->>]生产了任务：taskName11，优先级是：16
[Thread-生产者-->>]生产了任务：taskName12，优先级是：2
[Thread-生产者-->>]生产了任务：taskName13，优先级是：10
[Thread-生产者-->>]生产了任务：taskName14，优先级是：18
[Thread-生产者-->>]生产了任务：taskName15，优先级是：5
[<<--Thread-消费者]消费了任务：taskName14，优先级是：18
[Thread-生产者-->>]生产了任务：taskName16，优先级是：13
[Thread-生产者-->>]生产了任务：taskName17，优先级是：4
[Thread-生产者-->>]生产了任务：taskName18，优先级是：3
[Thread-生产者-->>]生产了任务：taskName19，优先级是：19
[<<--Thread-消费者]消费了任务：taskName19，优先级是：19
[<<--Thread-消费者]消费了任务：taskName6，优先级是：16
[<<--Thread-消费者]消费了任务：taskName11，优先级是：16
[<<--Thread-消费者]消费了任务：taskName9，优先级是：15
[<<--Thread-消费者]消费了任务：taskName16，优先级是：13
[<<--Thread-消费者]消费了任务：taskName2，优先级是：12
[<<--Thread-消费者]消费了任务：taskName4，优先级是：11
[<<--Thread-消费者]消费了任务：taskName3，优先级是：11
[<<--Thread-消费者]消费了任务：taskName13，优先级是：10
[<<--Thread-消费者]消费了任务：taskName8，优先级是：8
[<<--Thread-消费者]消费了任务：taskName7，优先级是：7
[<<--Thread-消费者]消费了任务：taskName15，优先级是：5
[<<--Thread-消费者]消费了任务：taskName17，优先级是：4
[<<--Thread-消费者]消费了任务：taskName18，优先级是：3
[<<--Thread-消费者]消费了任务：taskName12，优先级是：2

Reference

Java&Kotlin, Java数据结构
Java数据结构
本文由作者按照 CC BY 4.0 进行授权